PyTorch Geometric 탐구 일기 - Message Passing Scheme (1)

다음 글은 PyTorch Geometric 라이브러리 설명서에 있는 Creating Message Passing Networks 를 참고하여 작성했습니다.

PyTorch Geometric 레퍼런스와 소스코드를 뜯어보며 정리한 글(의식의 흐름)입니다.

• Graph Data in PyG
• Message Passing Scheme
• MessagePassing class
  • MessagePassing Class란?
  • Class 상속 관계
• MessagePassing Class in details
  • MessagePassing Class - 정의(init)
  • MessagePassing - propagate()
  • MessagePassing - message()
  • MessagePassing - update()
• Message Passing 구성해보기
  • Graph Convolution Neural Network
• Reference

Graph Data in PyG

그래프는 노드와 엣지의 집합으로 이루어져 있습니다. 그래서 보통 표현하기를, G=(V, E)와 같은 형태로 표현합니다. 하지만, 컴퓨터가 graph를 저장하는 방식으로 인해, E를 edge set을 indices 형태로 저장하게 됩니다. 또한, 노드나 엣지의 feature가 있을 수 있습니다. 따라서 그래프를 크게 indices matrix와 feature matrix로 표현할 수 있습니다.

PyTorch Geometric의 경우, 다음과 같이 그래프를 정의하고 있습니다.

• 주어진 sparse 그래프 $\mathcal{G}$는 다음과 같은 형태로 표현됩니다.
  • $\mathcal{G}$ = $(\mathrm{X, (I, E)})$)
    • node features : $\mathrm{X} \in \mathbb{R}^{|V|\times{F}}$
    • edge indices : $\mathrm{I} \in \{1,…,N\}^{2 \times{|E|}}$
    • (optinal) edge features : $\mathrm{E} \in \mathbb{R}^{|E|\times{D}}$

그림을 통해 간단한 예시를 살펴보겠습니다.

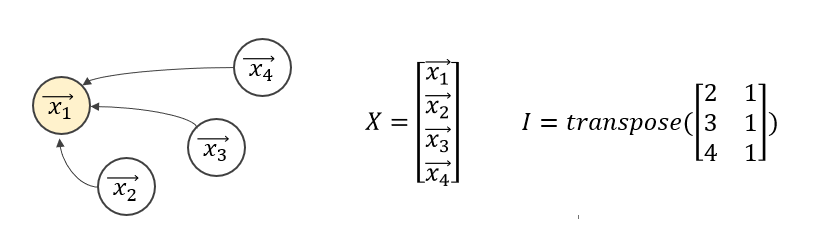
• 이처럼 그래프의 연결 관계는 edge_indices matrix $\mathrm{I}$로 표현가능합니다.
• 각 노드의 feature들은 $\vec{x_1} = [0.9, 0.3, 0.4]$처럼 벡터 형태로 표현될 수 있고, 이들을 모은 행렬이 바로 node features $\mathrm{X}$입니다.
  

Message Passing Scheme

GNN의 핵심 특징 중 하나로 node embedding이 이루어지는 방식을 말합니다. PyG에서는 다음과 같은 방식으로 Message Passing을 일반화하고 있습니다.

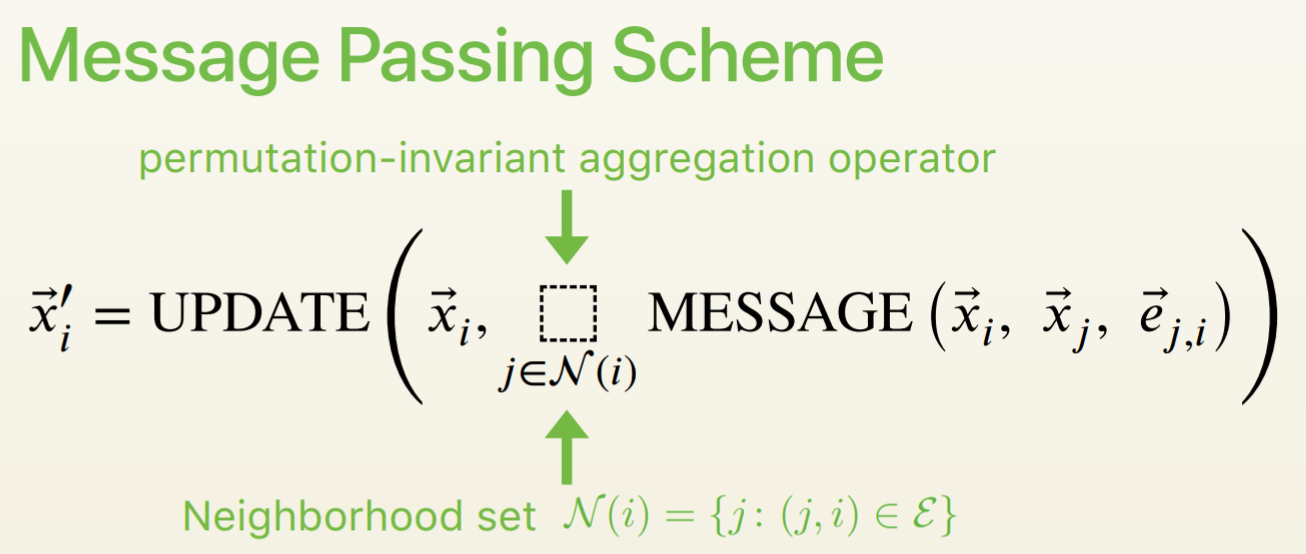
그림의 수식처럼, 주변 노드들과 연결된 엣지의 정보를 기준으로 MESSAGE를 구성하여, aggregate한 뒤, 타겟 노드의 임베딩을 UPDATE해주는 구조를 갖고 있습니다. 조금 더 자세하게, 아래와 같은 수식으로 일반화하여 표현합니다.

$ \mathbf{x}_i^{(k)} = \gamma^{(k)} (x_i^{(k-1)}, \square_{j \in N(i)} \phi^{(k)} (\mathbf{x}_i^{(k-1)}, \mathbf{x}_j^{(k-1)},\mathbf{e}_{j,i} )) $

• $x$ : node embedding
  • k=1인 경우, 각 노드의 input feature로 생각
• $e$ : edge features
  • edge feature가 connectivity 이외의 feature가 없는 경우, 그래프의 edge index로 보면 됨
• $\phi$ : message function
• $\square$ : aggregation function
• $\gamma$ : update function
• superscript (위첨자) : 레이어의 인덱스

MessagePassing class

PyTorch Geometric에서는torch_geometric.nn.MessagePassing이라는 base class를 통해 Message Passing을 구현할 수 있습니다.

MessagePassing Class란?

• GNN의 MessagePassing Shceme에 대해, propagation을 구조적으로 연결해주는 편리한 클래스
• 사용자는 message(), update()에 대해서 주로 설정해주면 됨
  • aggregation도 편한대로 설정(기본적으로는 add, mean, max 3가지가 있고, add가 기본)

Message Passing interface 예시

1
2
3
4
5
6
7
8
9

class MyOwnConv(MessagePassing):
    def __init__(self):
        super(MyOwnConv, self).__init__(aggr='add') # add, mean or max aggregation
        
    def forward(self, x, edge_index, e):
        return self.propagate(edge_index, x=x, e=e) # pass everything needed for propagation
    
    def message(self, x_j, x_i, e): # Node features get automatically mapped to source(_j) and target(_i) nodes
        return x_j * e 

Class 상속 관계

• torch.nn.Module이 superclass
• 따라서, 다음과 같은 구조를 가지는 것을 알 수 있음
  • torch.nn.Module $\Rightarrow$ torch_geometric.nn.MessagePassing $\Rightarrow$ OurCustomLayer
• 대부분의 torch_geometric.nn.conv layer 구현체들이 Message Passing Scheme을 따름

MessagePassing Class in details

해당 소스는 이 Link에서 확인할 수 있습니다.

MessagePassing Class - 정의(init)

• torch_geometric.nn.MessagePassing(aggr="add", flow="source_to_target")
  • 해당 소스 코드 참고함 (MessagePassing.__init__ 부분)
  • aggr : 각 노드간의 message를 어떻게 aggregation할지 결정
    • default 값은 “add”
    • “add”, “mean”, “max”, “None”로 선택가능
  • flow : message를 어떤 방향으로 흐르게 할지 결정
    • default 값은 “source_to_target”
    • “source_to_target”, “target_to_source”로 선택가능
    • 주변노드로부터 전달받을지 전달할지 결정한다는 의미
    • 일반적인 상황의 $e_{ij}$에 대해서, 다수의 source $j$가 target $i$로 정보를 전달해주는 흐름
  • node_dim : 노드의 차원을 의미
    • defualt 값은 int 0
    • 어떤 axis로 propagate할지 결정하는 것
  • support
    • self.__explain__, self.__edge_mask__ : GNNExplainer를 위해 추가 (최근)
    • self.__record_propagate__, self.__records__ : TorchScript를 위해 추가

MessagePassing - propagate()

• propagate(edge_index, size=None, **kwargs)

• 이 함수 호출 시, message()와 update() 함수를 차례로 호출하게 됨
  • 소스코드 중 일부 발췌

  1 2 3 4 5 6 7 8 9 10 11

  def propagate(): if mp_type == 'adj_t' and self.fuse and not self.__explain__: out = self.message_and_aggregate(edge_index, **msg_aggr_kwargs) # Otherwise, run both functions in separation. elif mp_type == 'edge_index' or not self.fuse or self.__explain__: msg_kwargs = self.__distribute__(self.inspector.params['message'], coll_dict) out = self.message(**msg_kwargs) out = self.aggregate(out, **aggr_kwargs) out = self.update(out, **update_kwargs)

  • message와 aggregate 함수는 분리되거나 합쳐져 사용
  • 최종적으로 update 함수를 통해 출력값 생성

• bipartite graph처럼 ($N,M$) 사이즈도 propagate 가능함

  • 이 경우, size = ($N, M$) 으로 넣어줌 (size가 Optional[Tuple[,]] 형태의 custom Type)

MessagePassing - message()

1
2
3

def message(self, x_j: torch.Tensor) -> torch.Tensor:
    # need to construct
    return x_j

• message(**kwargs)
  • 각 edge마다 발생하는 “message”라는 것을 어떻게 construct할지 구체화하는 함수
  • propagate의 호출을 따르므로, propagate에 전달할 어떤 인자든 넘길 수 잇음
  • 주의할 점, 메세지 간의 노드를 구체화할 때는, “_i”와 “_j”를 구분해서 표현해야 mapping이 정의 가능
    • flow=’source_to_target’일 경우, $e_{ij} \in E$ 로 구분
    • flow=’target_to_source’일 경우, $e_{ji} \in E$ 로 구분
• 따라서, 함수의 argument naming이 중요

MessagePassing - update()

1
2
3

def update(self, inputs: torch.Tensor):
    # need to construct
    return inputs

• 각 노드 $i$에 대해서, node embedding을 업데이트하는 함수
• Message Passing Formula에서 $\gamma$에 해당
• update(aggr_out, **kwargs)
  • message의 agreegation 결과값을 inputs 인자로 취함
  • 처음 propagate()에 전달한 초기 인자들도 이용 가능

Message Passing 구성해보기

Graph Convolution Neural Network

GCN Layer는 다음과 같은 Message Passing Formula로 정의할 수 있습니다.

$\mathbf{x}_i^{(k)} = \sum_{j \in \mathcal{N}(i) \cup { i }} \frac{1}{\sqrt{\deg(i)} \cdot \sqrt{\deg(j)}} \cdot ( \mathbf{\Theta} \cdot \mathbf{x}_j^{(k-1)} )$

• weighted matrix $\mathbf{\Theta}$
• 순서
  • 1) adjacency matrix에 self-loop 추가 (본인 노드 feature도 넣어줌)
  • 2) linearly transform node feature matrix
  • 3) compute normalization coefficients
  • 4) normalize node features ~ $\phi$
  • 5) sum up nbd node features (aggr=’add’)
  • 6) return new node embeddings ~ $\gamma$
• 1~3 과정은 즉, sum 기호 내부까지는 타겟 노드에 전달해줄, 흐르게 할 (propgating할) message를 construct하는 과정임
• 4~6 과정은 nbd인 node-pair에 대해 aggregation하고 해당 타겟 노드를 update하는 과정을 의미함

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40

import torch
from torch_geometric.nn import MessagePassing
from torch_geometric.utils import add_self_loops, degree

class GCNConv(MessagePassing):
    def __init__(self, in_channels, out_channels):
        super(GCNConv, self).__init__(aggr='add')
        self.lin = torch.nn.Linear(in_Channels, out_channels)
        
    def forward(self, x, edge_index):
        # x has shape [N, in_Channels]
        # edge_index has shape [2, E]
        
        # Step 1 : Add self-loops to the adjacency matrix
        edge_index, _ = add_self_loops(edge_index, num_nodes=x.size(0))
        
        # Step 2 : Linearly trasnform node feature matrix
        x = self.lin(X)
        
        # Step 3 : Compute normalization
        row, col = edge_index # [2, E]
        deg = degree(row, x.size(0), dtype=x.dtype)
        deg_inv_Sqrt = deg.pow(-0.5)
        norm = deg_inv_sqrt[row] * deg_inv_sqrt[col]
        
        # Step 4-6 : Start propagating messages
        return self.propagate(edge_index, size=(x.size(0), x.size(0)), x=x,
                              norm=norm)
    
    def message(self, x_j, norm):
        # x_j has shape [E, out_channels]
        
        # Step 4 : NOrmalize node features
        return norm.view(-1, 1) * x_j
    
    def update(self, aggr_out):
        # aggr_out has shape [N, out_channels]
        
        # Step 6 : Return new node embeddings
        return aggr_out 

위에서 정의한 GCNConv Class를 다음과 같이 사용할 수 있습니다.

1
2

conv = GCNConv(in_channels=16, out_channels=32)
x = conv(x=x, edge_index=edge_index)

PyTorch Geometric에 구현되어 있는 GCN Layer에 대해 좀 더 알아보고 싶다면, 아래 링크를 참조하시면 됩니다.

• torch_geometric.nn.GCNConv Source Code
• 데이터를 활용해 실제 GCN 모델을 돌려볼 수 있는 tutorial Code Link

Reference

• Fast Graph Representation Learning with PyTorch Geometric
• PyTorch Geometric Source Code
• Hands-on Graph Neural Networks with PyTorch & PyTorch Geometric