해당 글은 Algorithms. by S. Dasgupta, C.H. Papadimitriou, and U.V. Vazirani 를 정리한 스터디 노트입니다.
Chapter 4 Paths in graphs
4.1 Distances
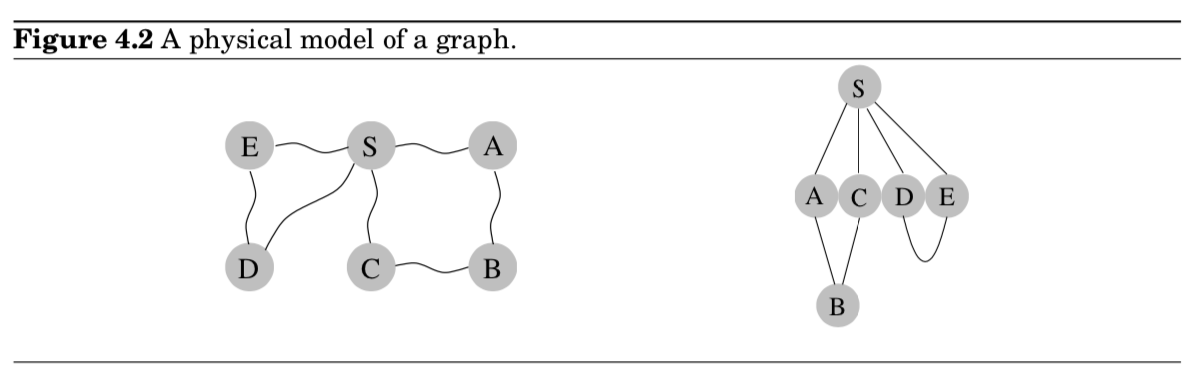
- DFS에 의해, 정점(starting point)로부터 도달가능한 그래프의 모든 노드들을 identify 가능함
- 하지만, 이러한 paths가 economical한 것은 아님 (위 그림과 같이)
- (LHS) $S$와 $C$ 사이의 실거리는 1인데
- (RHS) DFS의 search tree에 따르면 길이가 3임
distance between two nodes = the length of the shortest path between them
- 이 개념을 물리학적으로 묘사해볼 수 있음
- 하나의 vertex $s$를 손으로 잡고 나머지를 다 늘려뜨리기
- 어떤 특정 점까지의 거리는 $s$ 아래로 걸려있는 거리가 얼마나 인지랑 같음 (아래 그림)

- $dist(B, S)=2$
- 2 shortest paths
- 오른쪽 그림은 $S$를 손으로 들어올려서 taut하게 만든 그림
- edge $(D,E)$는 shortest path에 어떤 역할도 없고 slack으로 남음
4.2 Breadth-first search
정점 $s$로부터 거리를 계산하는 가장 편한 방법 : proceed layer by layer
- 거리가 $0, 1, 2, …, d$인 노드들을 골라냈다면, 거리가 $d+1$인 노드들은 쉽게 결정 가능
- 거리가 $d$인 노드에 인접(adjacent)하면서, 아직 안 본(as-yet-unseen) 노드들이 되기 때문
- 이를 통해, iterative algorithm을 설계할 수 있음 (2 layers가 동작하는 방식으로)
- 확실히 알아낸, 어떤 layer $d$가 있고, 그 layer의 nbs를 살펴보면서 발견하게 되는 $d+1$ layer가 존재함

- BFS 알고리즘은 위의 layer by layer로 단순히 동작하는 알고리즘임
- 동작 방식
- (초기화) queue $Q$는 정점 $s$로만 구성, 이 때 이 노드의 거리는 0
- for each subsequent distance $d=1,2,3,…,$ there is a point in time at which $Q$ contains all the nodes at distance $d$ and nothing else.
- As these nodes are processed (ejcected off the front of the queue), their as-yet-unseen neighbors are injected into the end of the queue.
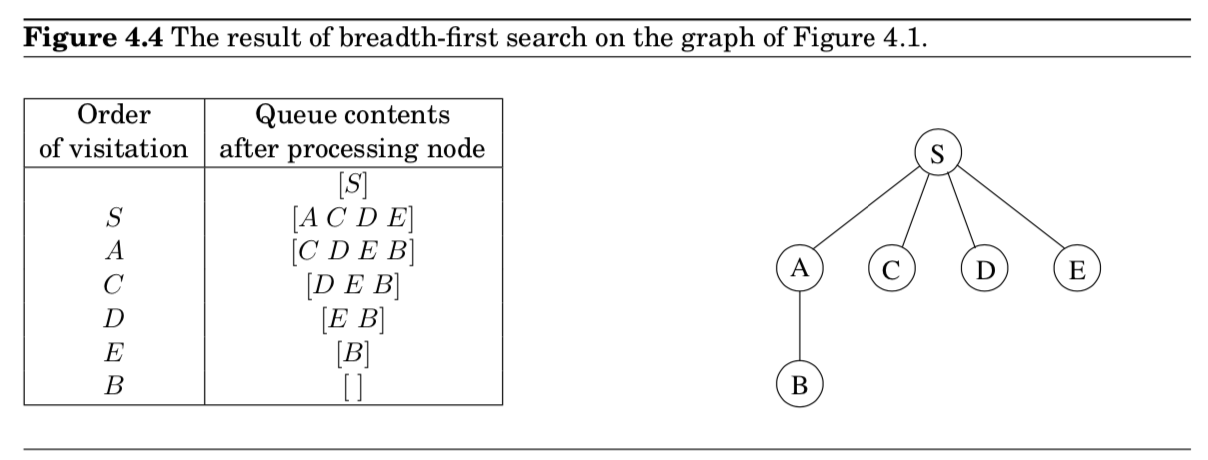
- 예제(Figure 4.1)에 적용
- DFS와 다르게, $S$로부터 출발하는 모든 paths들은 shortest임 (DFS-search tree와 다름)
- 따라서, shortest-path tree 라고 할 수 있음
- A rooted tree with root $s$.
Correctness
- BFS에서 돌아가는 basic intuition = layer by layer + checking as-yet-unseen nodes (adjacent)
- 알고리즘의 정합성을 체크하기 위해서는 아래와 같은 내용을 체크해야 함
- $\texttt{For each }d=0,1,2,…, \texttt{there is a moment at which}$
$(1) \texttt{ all nodes at distance} \leq d \texttt{ from }s \texttt{ have their distances correctly set}$
$(2) \texttt{ all other nodes have their distances set to } \infty;$
$(3) \texttt{ the queue contains exactly the nodes at distance } d.$ - 증명하기 위해서는, inductive argument in mind (for each $d$).
- $\texttt{For each }d=0,1,2,…, \texttt{there is a moment at which}$
Efficiency
- The overall running time of Algorithm : linear, $O(|V|+|E|)$
- 알고리즘 시간 = DFS와 동일한 이유
- 모든 노드가 큐에 정확히 한 번씩 존재함 (inject, eject 연산)
$\therefore$ $2|V|$ queue operations - 나머지는 알고리즘의 내부에 동작하는 loop에서 걸림 (checking adjacency)
- 각 edge들을 한번씩 훑음 (in directed graphs)
- 각 edge들을 두번씩 훑음 (in undirected graphs)
$\therefore$ $O(|E|)$ time
DFS versus. BFS
- DFS
- deep incursions into a graph, retreating only when it runs out of new nodes to visit
- (+) : wonderful, subtle, and extremely useful properties (we saw in Chapter 3)
- (-) : can end up taking a long and convoluted route to a vertex that is actually very close by
- BFS
- visit vertices in increasing order of their distances from the starting point ($s$)
- borader, shallower search
- almost exactly the same code as DFS (but with a queue in place of a stack)
- Note (stylistic difference), (less important)
- BFS : do not restart the search in other connected components
- actually, we are interested in distances from $s$
- so that nodes not reachable from $s$ are simply ignored.
- BFS : do not restart the search in other connected components
4.3 Lengths on edges
- BFS는 모든 edges들을 동일 길이로 취급했지만, 이건 실제로 굉장히 드문 상황임
- In applications where shortest paths are to be found
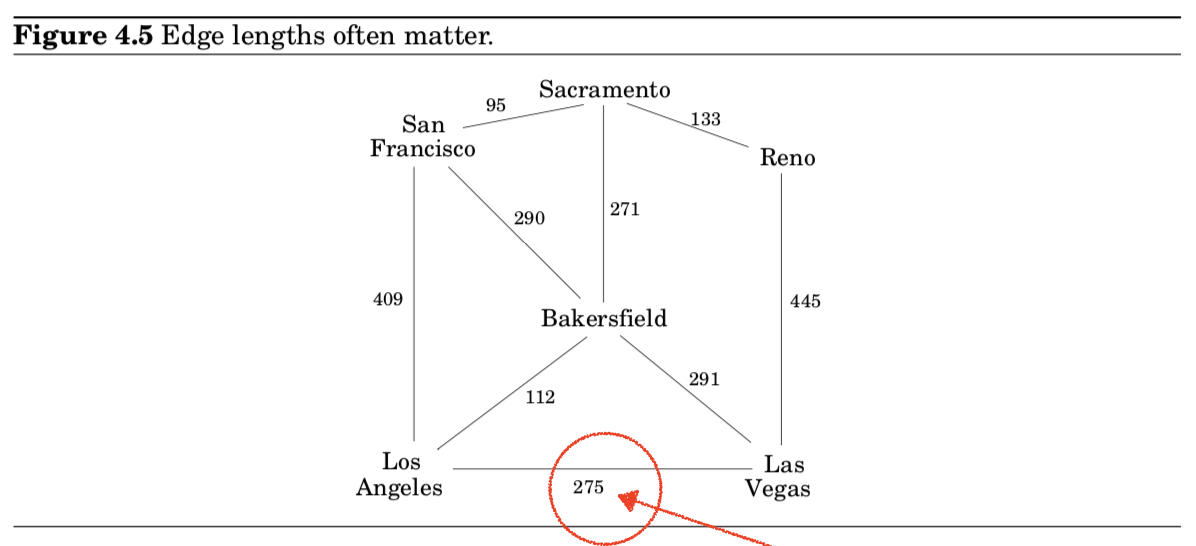
- 예시 (Figure 4.5)
- San Francisco 에서 Las Vegas로 가는 가장 빠른 길을 찾고 싶은 상황
- 이런 경우를 고려하여, 모든 edge $e \in E$에 대해서, $l_e$라는 길이를 갖고 있다고 annotate함
- $l(u,v)$나 $l_{uv}$라고 표현하기도 함
- $l_e$가 항상 물리적인 길이를 표현할 필요는 없음
- Time, money와 같은 어떤 quantitiy가 됨
- negative lengths도 됨
4.4 Dijkstra’s algorithm 


4.4.1 An adaptation of breadth-first search
- 앞에서 본 BFS의 상황을 더 일반화해보자
- a graph $G=(V,E)$ , whose edges lengths $l_e$ are positive integers
A more convenient graph
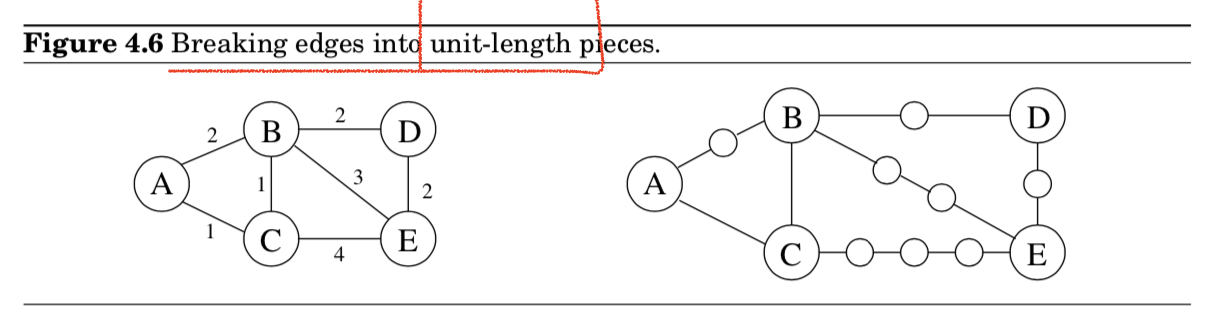
- 그래프를 바꾸는 간단한 트릭을 이용해서, BFS를 적용할 수 있음
- 더미 노드를 추가! ( =$G$의 edges들을 unit-length를 가지는 조각들로 쪼갬)
- 정리하자면 기존의 $G$를 다음의 방법으로 새로운 $G’$으로 만든다.
- $\texttt{For any edge }e=(u,v) \texttt{ of }E, \texttt{ replace it by }l_e \texttt{edges of length 1,}$
$\texttt{by adding }l_e - 1 \texttt{ dummy nodes between }u \texttt{ and }v.$
- $\texttt{For any edge }e=(u,v) \texttt{ of }E, \texttt{ replace it by }l_e \texttt{edges of length 1,}$
- 이렇게 변환한 $G’$은 우리가 관심있는 노드 집합 $V$에 대해서, 기존 $G$와 같은 distances를 유지할 수 있음
- 중요한 사실은 $G’$이 모두 unit length를 가지므로, $G’$에 대해 BFS를 돌려서 $G$에 대한 거리를 계산할 수 있게 되는 것
Alarm clocks
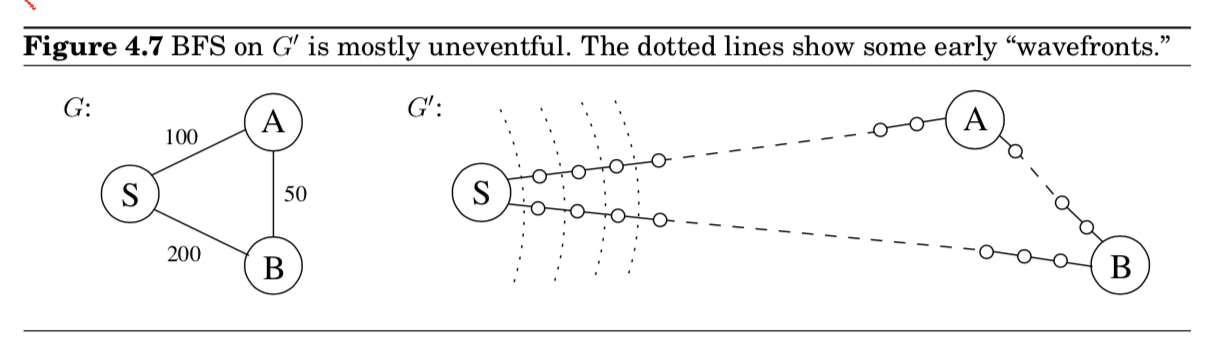
- 더미 노드 전략은 효율성 측면에서 문제가 있음
- $G’$이 더미 노드들이 많다 보니, 우리가 고려하지 않아도 될 노드들의 거리까지 계산한다는 문제가 존재
- $G’$의 정점 $s$로부터 시작해서 BFS를 한다고 가정 (단위분당 단위거리)
- 처음 99분동안은 $S-A$와 $S-B$를 따라서 지루하게 알고리즘 progress (끝없는 더미의 향연)
- 이런 지루한 과정 동안은 재우고, 흥미로운 일이 일어날 때만 깨우는 알람이 있으면 어떻게 될까?
- 구체적으로, 기존 그래프 $G$에 존재하는 노드들 중 하나를 만나게 될 때를 의미
- $G’$이 더미 노드들이 많다 보니, 우리가 고려하지 않아도 될 노드들의 거리까지 계산한다는 문제가 존재
- “alarm clock algorithm”의 intution
- 처음 시작할 때, 두 개의 알람을 세팅
- 노드 $A$에 대해서 $T=100$
- 노드 $B$에 대해서 $T=200$
- 이 $T$값들은 $estimated \; times \; of \; arrival $ 로, 현재 travered 중인 엣지들 위를 기반으로 산정됨
- $A$를 찾기 위해서 먼저 재웠다가 $T=100$ 때 깨우는 구조임
- 이 시점에서, $B$에 도착 측정 시간(estimated times of arrival)은 $T=150$으로 변경되므로, 알람 또한 바꿈
- 처음 시작할 때, 두 개의 알람을 세팅
- “alarm clock algorithm” generalization
- “alarm clock algorithm”

Dijkstra’s algorithm
- 이 알고리즘에 적합한 자료구조는 $priority \; queue$ (usually implemented via a $heap$)
- 어떤 측면에서?
- 1) maintains a set of elements (nodes) with associated numeric key value (alarm times)
- 2) supports the following opeartions:
$Insert$ : 집합에 새로운 원소를 추가
$Decrease-key$ : 특정 원소의 키값 감소를 수용(Accmmodate the decrease in key value of a particular element)
$Delete-min$ : 가장 작은 키값을 가진 원소를 반환하고, 집합에서 해당 원소를 삭제
$Make-queue$ : Build a priority queue out of the given elements, with the given key values (In many implementations, this is significantly faster than inserting the elements one by one.)- (The name decrease-key is standard but is a little misleading: the priority queue ttypically does not itself change key values. What this procedure really does is to notify the queue that a certain key value has benn decreased)
- 어떤 측면에서?



4.4.2 An alternative derivation
Compute shortest paths
정점 $s$(시작)으로부터 점차 밖으로 확장해나감 = 어떻게? 거리와 최단 경로를 아는 그래프 지역을 늘리면서…
-
구체적으로 구하는 방법
- “known region”을 생각, $R$
- $s$를 포함하는 노드들의 집합 $R$이 될 때, 다음에 추가될 것은 $s$로부터 가장 가까우면서, $R$ 밖에 있는 노드들이 되어야 할 것
- 이러한 노드들을 $v$라고 하면, 어떻게 식별할 수 있을까?
- $s$에서 $v$까지 가는 최단 경로 안에서 $v$ 바로 이전의 노드를 $u$라고 하자.
- 모든 edge length가 양수라고 가정
- $u$는 $v$보다 $s$에 가까울 것임 => $u$ 는 $R$에 들어있음
- 그래서 $s$에서 $v$로 가는 최단 경로는, $a \; known \; shortest \; path \; extended \; by \; a \; single \; edge$라고 할 수 있음

4.4.3 Running time
- 다익스트라 알고리즘은 구조적으로 BFS와 동일함
- 하지만, 우선순위 큐가 계산량을 더 많이 요구하기 때문에 느림
- (BFS의 경우) $\texttt{eject}$와 $\texttt{inject}$ → constant-time
- 총 연산량 : $|V| \; \texttt{deletemin}$와 $|V|+|E| \; \texttt{insert/decreasekey}$
- $\texttt{makequeue}$에 최대 $|V| \texttt{insert}$ 연산이 들어가기 때문에
- 이 시간복잡도는 어떻게 구현하냐에 따라 다를 수 있음
- binary heap을 사용할 경우 총 걸리는 시간은 $O((|V|+|E|)\log{|V|})$
Which heap is best?
4.5 Priority queue implementations
4.5.1 Array
- 우선 순위 큐의 가장 간단한 형태
- an unordered array of key values for all potential elements(the vertices of the graph, in the case of Dijkstra’s algorithm)
- 초기에, 이 값들은 $\infty$로 설정
- $\texttt{insert}$나 $\texttt{decreasekey}$는 $O(1)$로 속도가 빠름
- because it just involves adjusting a key value
- $\texttt{deletemin}$ 는 리스트의 linear-time 스캔이 필요함
4.5.2 Binary heap
4.5.3 $d$-ary heap
4.6 Shortest paths in the presence of negative edges
4.6.1 Negative edges
Intro
- edge의 길이가 음수
- 다익스트라 알고리즘이 부분적으로 동작하는 이유
- 시점($s$)로부터 어떤 노드 $v$로 가는 가장 짧은 경로는 $v$보다 가까운 노드들만 지나가기 때문
- 이는 edge의 길이가 음수가 될 때는 성립하지 않는 이야기임
- Figure 4.12의 경우, 가장 짧은 경로는 더 멀리 지나갈 수 있다는 사실을 볼 수 있음
- 다익스트라 알고리즘이 부분적으로 동작하는 이유
- 새로운 상황을 어떻게 해결할 수 있을까?
- 다익스트라 알고리즘을 이용하자!
- 변하지 않는 사실 : $\texttt{dist}$ 값은 정확하거나 높게 측정된 경우 2가지 밖에 없음
- 시작은 $\infty$에서 시작
- 거리값이 바뀔 때는 오직 edge를 따라 다음과 같이 업데이트 될 때
$\texttt{procedure update}((u,v)\in E)$
$\texttt{dist}(v) = \min{ \{ \texttt{dist}(v), \texttt{dist}(u) + l(u,v) \} }$
- 이 update 함수는 단순한 사실을 이용한 것임
- $v$까지의 거리는 $u$까지 거리와 $l(u,v)$를 더한 값보다 더 클 가능성이 없다.
- 그리고 update는 다음과 같은 2가지 특성이 있음
- 1) 아래의 경우에 $v$까지의 정확한 거리를 줄 수 있음
- $v$로 가는 가장 짧은 경로 속 2번째 노드가 $u$인 경우
- $\texttt{dist}(u)$가 정확한 경우
- 2) $\texttt{dist}(v)$를 너무 작게 만들지 못한다는 관점에서, $safe$하다고 말할 수 있음
- 즉, 엄청 많은 수의 update문에 영향을 받지 못함
- (= 즉, 해가 되는 연산이 아니고, 적절한 상황에서 잘 사용한다면 올바른 거리 값을 구할 수 있다는 뜻)
- 1) 아래의 경우에 $v$까지의 정확한 거리를 줄 수 있음
- 사실, 다익스트라 알고리즘은 $\texttt{update}$를 단순히 나열한 것으로도 볼 수 있음
- 이 단순한 나열이 negative edges에선 동작하지 않음
- 하지만, 가능하게 하는 특정 시퀀스가 존재한다면?
- 노드 $t$를 하나 고르고, $s$에서 출발하는 가장 짧은 경로를 확인
- 이 경로는 최대 $|V|-1$ edges를 가짐
- 만약 경로에 존재하는 edges들이 최단 경로 방향 순으로 잘 update가 되었다고 한다면, $t$는 올바르게 계산될 것이다.
- 이 엣지들에 다른 업데이트가 발생해도 크게 문제는 없음 + 다른 부분에 업데이트가 발생해도 문제는 없음
- update가 safe하다는 특성 때문에
- 그래도 여전히 문제가 남음
- 올바른 순서대로 올바르게 업데이트할 수 있을지에 대한 보장이 없음
- 단순하게, 모든 edges들에 대해 $|V|-1$번 업데이트를 해버리자.
- 이렇게 되면, $O(|V| \cdot |E|)$의 시간복잡도를 가짐
- Bellman-Ford algorithm이라고 부름 (Figure 4.13)
- example (Figure 4.14)

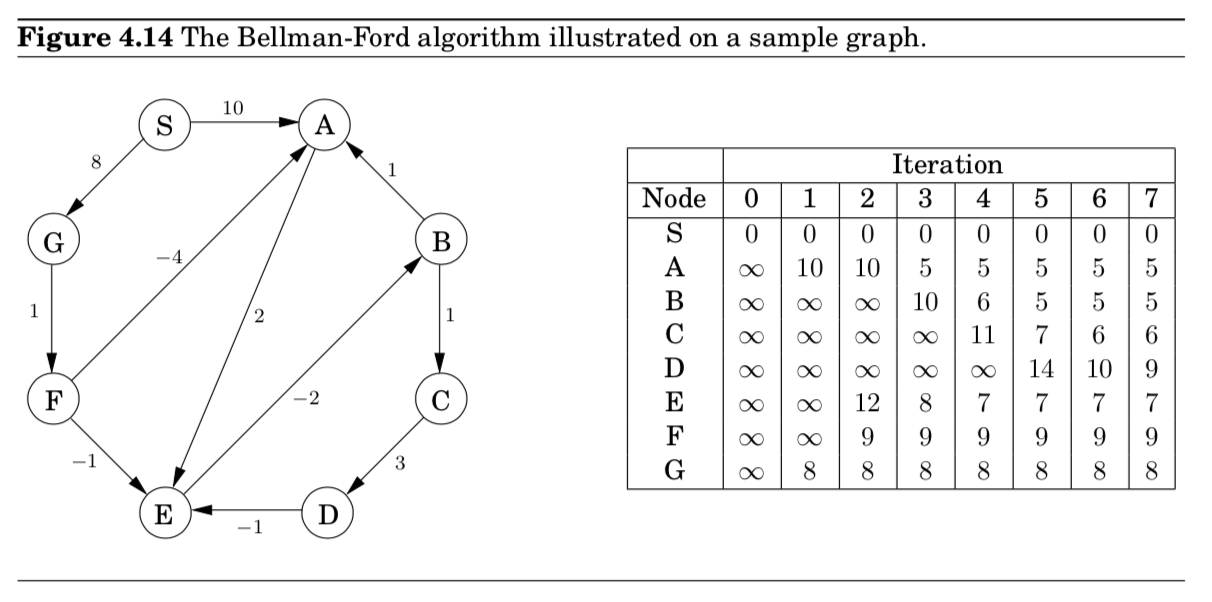
note
- 어떤 정점으로부터 최소 경로의 최대 엣지 갯수는 V-1니까, 그거보다 작을 때가 많음
- 따라서, SP 알고리즘에 extra 체크해주는 작업을 추가해주는게 말은 됨
- 어떤 작업이냐면, 더이상의 업데이트가 일어나지 않는 경우 terminate
4.6.1 Negative cycles
- 그래프에 negative cycle이 존재할 경우, 계속 반복해서 경로의 길이값을 낮출 수 있음 = ill-posed
- 기존의 SP 알고리즘은 이러한 사이클이 없는 경우에만 동작
- 이러한 가정이 어디서 왔을까?
- 바로, $s$에서 $t$로 가는 가장 짧은 경로의 존재성에 대해 언급했을 때임
- 이 negative cycle을 검출하는 방법을 생각할 수 있음
- $|V|-1$번의 루프를 수행하고 나서, 추가적으로 한 번더 루프를 돌림
- 이 루프를 돌렸을 때, 거리값의 변화가 있다면 negative cycle이 존재한다고 볼 수 있음
4.7 Shortest paths in dags
Introduction
- negative cycles의 가능성을 제외한다면, 그래프는 2가지의 서브 클래스가 있음
- 1) negative edges가 없는 그래프
- 2) cycles이 없는 그래프
- 이미, 1번째의 경우는 다뤘고, 이제 우리가 다룰 내용은 2번째 내용에 다룰 예정임

single-source shortest-path in DAG
- can be solved in just linear time
- need to perform a seq. of updates that includes every shortest path as a subseq.
- efficiency => DAG는 노드들을 linearized order할 수 있음 (topologically sort)
- 알고리즘 적용 (Figure 4.15)
- 1) DAG를 DFS에 의해 linearize할 수 있음
- 2) 정렬된 순서로 노드들을 방문
- 3) 각 노드들마다 노드의 edges를 update
- 이 방식은 positive에만 적용되는 것은 아님
- 이를 이용하면, 가장 longest paths를 찾을 수 있음
- 모든 길이들에 -부호로 뒤집어주면 끝
reference
Bellman-ford
BFS
- http://www.math.caltech.edu/~2014-15/1term/ma006a/class7.pdf
Especially, The Correctness of BFS (proof)
- https://www.cs.mcgill.ca/~pnguyen/251F09/BFScorrect.pdf
priority queue
