해당 글은 Algorithms. by S. Dasgupta, C.H. Papadimitriou, and U.V. Vazirani 를 정리한 스터디 노트입니다.
Chapter 6 Dynammic programming
- 앞에서 봤던 알고리즘들은 특정 타입에 대한 문제들에서만 사용가능하다는 단점이 있음
- divide-and-conquer
- graph exploration
- greed choice
- 알고리즘 방식의 sledgehammer 역할을 하는 두 가지 테크닉에 대해 살펴볼 것
- **dynamic programming **(6장에 해당)
- linear programming
6.1 Shortest paths in dags, revisited
- (Chapter 4)에서 shortest paths는 DAG형태로 쉽게 풀 수 있었음
- 이 shortest path in dags 에 대해 다시 살펴보려고 함 → DP의 중심을 이해하는데 도움이 됨
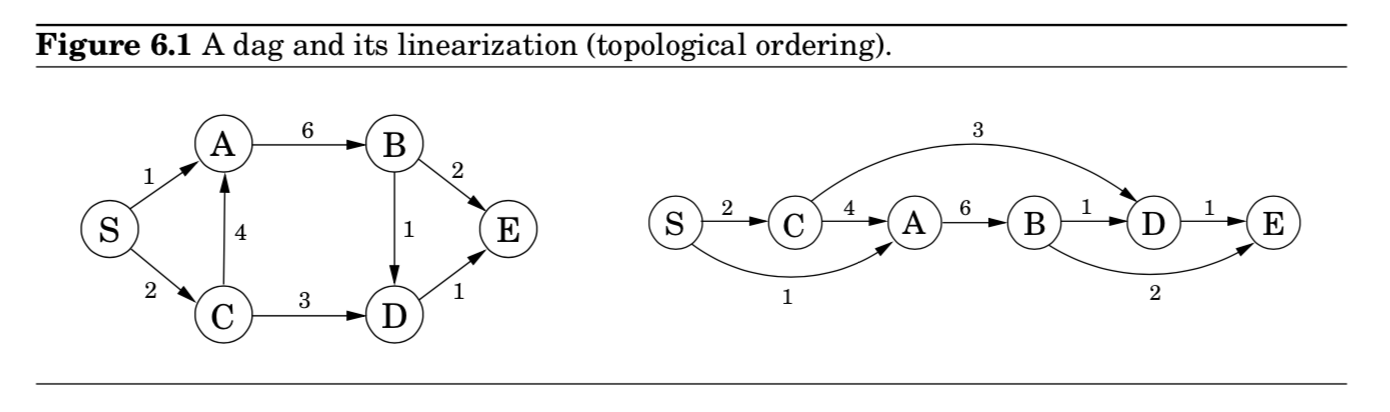
- DAG(directed acyclic graphs)의 특징을 이용해, 오른쪽 그림과 같이 노드들을 linearized하게 할 수 있음
- DAG를 linearized함으로써, 노드 $S$ (시작점) 로부터 다른 노드 사이의 거리를 알아내는데 도움을 줄 수 있음
- $D$까지의 거리를 알고 싶다면, predecessors인 $B$와 $C$를 조사
- 따라서, 2개의 길만 비교하기만 하면 됨
- $\text{dist}(D) = \min{\{\text{dist}(B)+1, \text{dist}(C)+3 \}}$
- 모든 노드에 대해 이러한 관계로 표현할 수 있음
- 만약 우리가, 위 그림의 왼쪽에서 오른쪽 방향으로 $\texttt{dist}$를 계산한다고 하면,
노드 $v$에 도달할 때까지, $\texttt{dist}(v)$를 계산하기 위해 필요한 모든 정보들을 이미 다 갖고 있다고 말할 수 있다. - 따라서, 모든 거리들을 단 하나의 single pass로 계산가능함 (아래와 같이)
- $D$까지의 거리를 알고 싶다면, predecessors인 $B$와 $C$를 조사
- $\texttt{initialize all dist}(\cdot)\texttt{ values to }\infty$
$\texttt{dist}(s) = 0$
$\texttt{for each }v \in V \smallsetminus \{s\}, \texttt{ in linearized order:}$
$\;\;\;\;\;\;\;\;\; \texttt{dist}(v) = \min_{(u,v)\in E} \{ \texttt{dist}(u) + l(u,v) \}$- 이 알고리즘은 $\{\text{dist}(u) : u \in V\}$라는 subproblems의 집합을 푸는 것과 같음
- $\texttt{dist}(s)$와 같이, 가장 작은 값으로 시작해, 점차 “larger” subproblems들을 점진적으로 해결해나감
- 이 과정속에서 $\min$을 $\max$로 바꾼다면, 가장 긴 paths를 찾는 것과 다름 없음
- 혹은, bracket 안의 덧셈을 곱셈으로 바꾼다면, edge lengths의 가장 작은 곱을 가지는 path를 찾는 것을 말함
- 이 알고리즘은 $\{\text{dist}(u) : u \in V\}$라는 subproblems의 집합을 푸는 것과 같음
Dynamic programming
- 어떤 한 Problem이 subproblems의 집합으로 생각해볼 수 있을 때, 가장 작은 것부터 하나씩 tackling하고, 그 답을 이용해 전체 problem이 풀릴 때까지 더 큰 subproblem들을 해결하는, 강력한 알고리즘 패러다임을 의미함
6.2 Longest increasing subsequences
문제 상황 (Longest increasing subsequence problem)
- 입력 : a $sequence$ of numbers $a_1, …, a_n$
- 설명 : $a \; subsequence$ : any subset of these numbers of the form $a_{i_1}, a_{i_2}, …, a_{i_k}$, where $1 \leq i_1 < i_2 < … < i_k \leq n$
- $increasing$ subsequence in which is getting strictly larger
- TASK : to find the increasing subsequence of greatest length
- 예시) $\text{5 - 2 - 8 - 6 - 3 - 6 - 9 - 7}$
- 가장 긴 증가 수열 찾기 : $2→3→6→9$
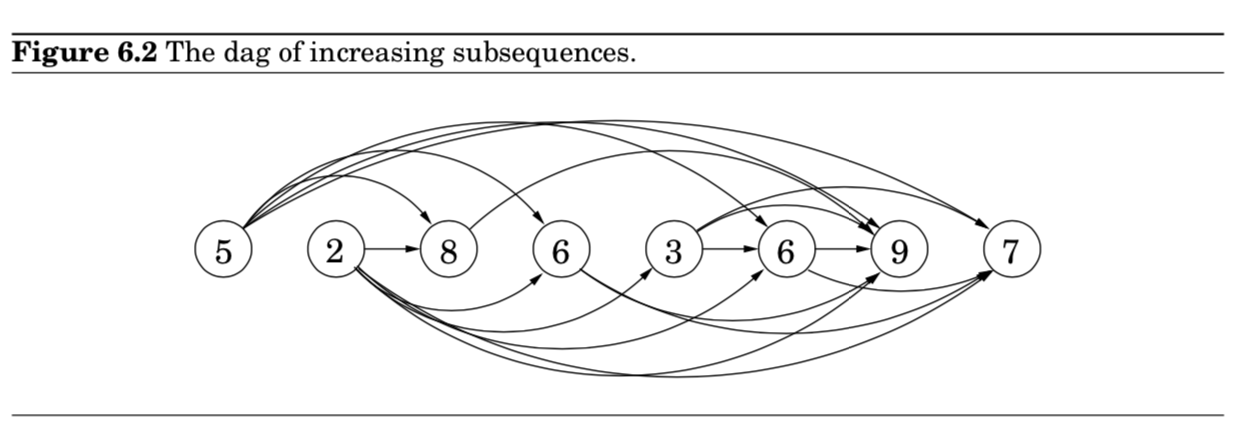
- solution space를 더 잘 이해하기 위해서, 가능한 모든 transitions를 가진 그래프를 그려보자.
- 각 $a_i$에 대해 노드 $i$를 생각
- $i<j \text{ and } a_i < a_j$를 만족하는, 가능한 모든 $a_i$와 $a_j$를 directed edges $(i,j)$로 연결
- 이렇게 되면, one-to-one correspondence가 존재
- between increasing subsequences and paths in dag.
- 결국, 우리의 목표는 dag 안에서 가장 긴 path를 찾는 것으로 단순화할 수 있게 된다.
Here is the algorithm:
$\texttt{for } j=1,2,…,n:$
$\;\;\;\;\;\;\;\; L(j) = 1 + \max{\{L(i) : (i,j) \in E\}}$
$\texttt{return } \max_j L(j)$
- 아까 shortest path 알고리즘을 이용
- edge weight가 모두 1이라고 생각하면 됨
- $\min \rightarrow \max$
- 노드 $j$까지 도달하기 위한 path들은 결국, $j$의 predecessors를 지나가야만 하므로,
$L(j)$는 predecessors의 $L(\cdot)$값의 maximum + 1이 됨 - $L(j)$는 가장 긴 path의 길이를 의미 = 가장 긴 증가 부분수열
In the view of DP
- 하나의 큰 문제를 해결하기 위해, subprobmes의 집합을 정의
- a collection of subproblems : ${L(j) : 1 \leq j \leq n }$
- 이 subproblems 다음과 같은 성질을 만족하는데, 이때문에 single pass가 가능하게 됨
- subproblems간의 order가 존재
- 이 ordering에 따라, 먼저 등장한 subproblems가 smaller함
- 이 smaller subproblems로 계속해서 다음 subproblem을 푸는 관계가 존재함
Analysis of Algorithm in DP’s view
- $j$의 predecessors를 필요로 함
- (Exercise 3.5) reverse graph $G^R$의 adjacency list에 대해서, linear time안에 구축 가능함
- $L(j)$의 계산은 $j$의 indegree에 비례하므로, 총 시간은 $|E|$에 linear하게 주어짐
- 이는, 최대 $O(n^2)$ (input array가 오름차순으로 정렬된 경우)
- 따라서 DP로 푸는 방식은 간단하면서 효율적임
- 더 구체적인 문제가 하나 남아있음
- $L$값을 계산하는 것은 결국, 길이를 계산한 것임
- 이를 다시 하나의 최적화된 수열값으로 복원하려면 어떻게 해야할까?
- Chapter4에서 shortest paths를 위해 사용했던 bookkepping device을 똑같이 이용해 처리
- $L(j)$를 계산하는 동안에, $\texttt{prev}(j)$를 따로 또 노트해둠
- $\texttt{prev}(j)$는 $j$로 가는 가장 긴 path에 놓여진 next-to-last node임
- 이러한 backpointers를 따라가면서 reconstructed하면 끝
Recursion? No, thanks.
- 가장 긴 부분 증가 수열 찾기 문제로 돌아가서 $L(j)$를 이용해 recursive algorithm을 구현할 수 있을까?
- 가능은 하지만, 좋은 아이디어는 아님.
- require exponential time!
- $L(j) = 1 + \max{\{L(1), L(2), …, L(j-1)\}}$ 라고 하자.
- $L(n)$를 구할 때 필요하기 위해 묘사된 트리는 exponentially many nodes를 가진다.
- 왜 분할 정복 알고리즘에서는 recursion이 잘 먹혔을까?
- 분할 정복 알고리즘에서는 하나의 작업이 물질적으로 더 작은 작업으로 표현 가능하기 때문이다.
- 문제 사이즈를 줄이기 때문에, 전체 recursion tree는 log 깊이와 polynomial number of nodes를 가지게 됨
- 반대로, DP 형태로 풀게되면, 문제는 slightly 작은 문제들로 줄여짐
- $L(j) \rightarrow L(j-1)$
- 따라서, recursion tree는 polynomial depth와 exponential number of nodes를 가지게 됨
- 하지만, 대부분의 노드가 반복되는 작업이고, 서로 다른 subproblems들이 많지 않다.
- 효율성은 이러한 명백한 subproblems를 뽑아내서 제대로 된 순서로 푸는데서 발생하게 된다.
Programming?
6.3 Edit distance
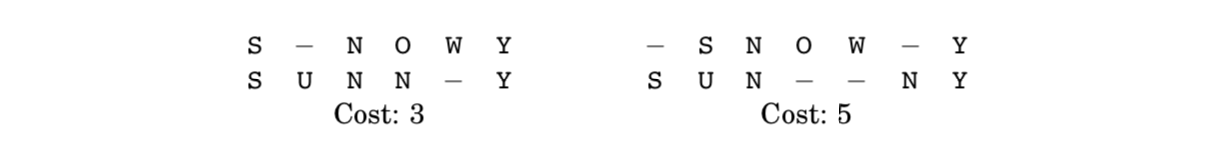
- $cost$ : 문자가 서로 다른 컬럼의 개수
- 두 문자열 사이의 $edit \; distance$는 그들의 best alignment의 $cost$를 말함
- 결국, Edit distance = minimum number of $edits$를 말함.
A dynammic programming solution
- DP로 problem을 해결할 때, 가장 중요한 것은 “무엇이 subproblems인가”를 정의하는 것
- 우리의 목표는 두 문자열 $x[1 \cdots m], y[1 \cdots n]$ 사이의 edit distance를 구하는 것
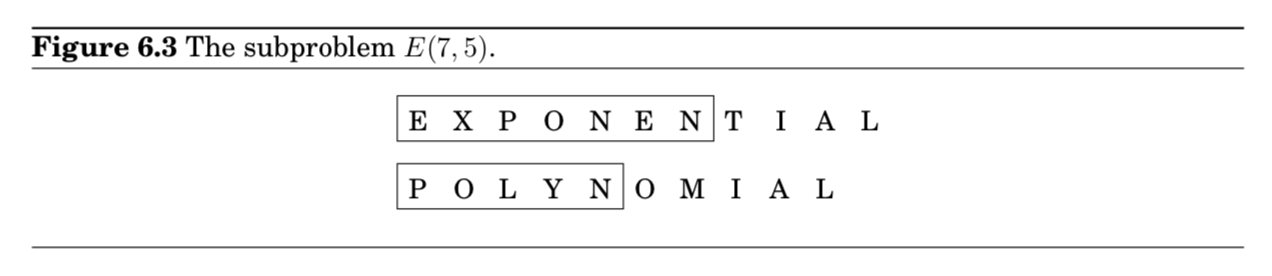
$prefix$로 생각해서 subproblem을 정의해볼 수 있음
subproblem $E(i,j)$는 $x,y$의 prefix에 대해 edit distance를 구하는 것임
- $x[1 \cdots i], y[1 \cdots j]$
그렇다면, $E(i,j)$를 더 작은 subproblems로 표현할 필요가 있음
먼저, $x[1 \cdots i], y[1 \cdots j]$ 사이 best alignment는 어떻게 될까? → $E(i,j)$
다른건 모르겠지만, 가장 오른쪽 컬럼은 총 3가지 경우가 나올 수 있음
- 1번
- 2번
- 3번
각각의 경우를 더 작은 subproblems로 해석할 수 있음
- 1번 → $E(i-1, j)$
- 2번 → $E(i, j-1)$
- 3번 → $E(i-1, j-1)$
결국, 3가지의 경우 중에서 뭐가 좋은지 모르니 다음과 같이 표기할 수 있음
$E(i,j) = \min{\{1+E(i-1,j), 1+E(i,j-1), \text{diff}(i,j) + E(i-1,j-1)\}}$
- 여기서, $\text{diff}(i,j)$ 는 $x[i]=y[j]$인 경우 0, 아니면 1을 뜻함 (차이가 있냐 없냐의 함수)
The underlying dag
모든 DP는 *underlying dag structure*를 갖고 있음
- node : a subproblem
edge : a precedence constraint on the order where the subproblems can be tackled
Having nodes $u_1, …, u_k$ point to $v$ means “subproblem $v$ can only be solved once the answers to $u_1, … u_k$ are known.”
- 예시) edit distance problem
- subproblem : $(i,j)$
- precedence constraints : $(i-1, j) / (i,j-1) / (i-1,j-1) \rightarrow (i,j)$
- 만약 edge에 weight를 준다면, edit distances는 dag 내부에서 가장 shortest paths를 구하는 것으로 생각할 수 있음
- 이 경우, 모든 edge는 1임. (except for $\{ (i-1, j-1) \rightarrow (i,j) : x[i] = y[j] \})$ = edge 0)
- 정리하면, s=(0,0)에서 t=(m,n)까지 가는 거리를 구하는 것과 같음
- 이 길을 가는동안, 각 움직임은 다음에 해당한다.
- down : deletion
- right : insertion
- diagonal : match or substitution
- 이렇게 DAG형태로 바꿈으로써, edit distance와 같은 action(insertions, deletions, and substitutions)를 일반화할 수 있음
Common subproblems
Of mice and men
6.4 Knapsack
문제 상황
- 도둑질할 때, 가치 있는 물건만 최대한 담아서 가방에 넣고 튀어야 함
- 가방에 최대 담을 수 있는 총 무게는 $W$
- 가져갈 수 있는 물건은 총 $n$개이며, 각각 무게$(w_i)$와 가격($v_i$)이 있음
- What’ the most valuable combination of items he can fit into his bag?
- 문제가 크게 2가지 버전이 있음 (물건 수량 관련)
- Chapter 8에서 보게 되겠지만, 두 가지 버전에 대해서, polynomial-time 알고리즘이 없을 것 같아 보임
- 하지만, DP를 사용한다면, 두 가지 버전 모두 $O(nW)$로 해결 가능
- $W$가 작을 때 reasonable하지만, input size가 오히려 $W$보다 $\log{W}$에 비례하기 때문에 polynomial이 아님
i) Knapsack with repetition
- DP 관점에서, subproblem을 어떻게 정의해야 할까?
- 반복이 허용되는 경우에는, 원래 problem을 2가지 방식으로 줄일 수 있음
- smaller kanpsack capacties $w \leq W$
- fewer items $j \leq n$
- subproblem 정의
- $K(w) = \text{maximum value achievable with a knapsack of capacity }w$
- $K(w)$의 OPT solution에서 물건 하나를 제거한다면, $K(w-w_i)$의 OPT solution이 됨.
- 즉, $K(w)$는 $K(w-w_i) + v_i$로 표현가능함
- $K(w) = \max_{i:w_i \leq w}{ \{ K(w-w_i)+v_i \}}$
- 반복이 허용되는 경우에는, 원래 problem을 2가지 방식으로 줄일 수 있음
Algorithm (Knapsack with repetition)
$K(0) = 0$
$\texttt{for }w=1\texttt{ to }W:$
$\;\;\;\; K(w) = \max{ \{ K(w-w_i) + v_i : w_i \leq w \}}$
$\texttt{return }K(W)$
- 위 알고리즘은 길이가 $W+1$인 1차원 테이블 표를 탐색함
- 그리고, 각각 연산을 수행하는데 있어 $O(n)$이 걸림
$\therefore$ 총 수행 시간 $O(nW)$ - DAG형태로 생각하면, the longest path in a dag를 푸는 문제와 동일
ii) Knapsack without repetition
- 반복이 허용되지 않는다면?
- i)에서 정의했던 subproblem은 무용지물
- $K(w-w_n)$ 시점에서 해당 물건($n$)의 선택 여부를 모르기 때문
- 따라서, 사용한 물건들에 대한 추가 정보를 변수로 담아야 함
- subproblem 정의
- $K(w,j) = \text{maximum value achievable using a knapsack of capacity }w \text{ and items }1,…j$
- 우리가 찾는 최종 해는 $K(W,n)$
- 다음과 같이 더 작은 subproblem으로 표현할 수 있음
- $K(w,j) = \max{\{K(w-w_j, j-1)+v_j, K(w,j-1)\}}$
- 즉, $K(W,j)$는 $K(\cdot, j-1)$로 표현됨
- 한 물건에 대해, 무게를 늘려가며 해당 무게의 최적 value를 구함
- 다음 물건으로 넘어가면 현상유지할지, 추가할지 고려해 max value 구함
- i)에서 정의했던 subproblem은 무용지물
Algorithm (Knapsack without repetition)
$\texttt{Initialize all }K(0,j)=0 \texttt{ and all }K(w,0)=0$
$\texttt{for }j=1 \texttt{ to }n:$
$\;\;\;\; \texttt{for }w=1 \texttt{ to }W:$
$\;\;\;\;\;\;\;\; \texttt{if }w_j>w: \;\;\;\; K(w,j)=K(w,j-1)$
$\;\;\;\;\;\;\;\; \texttt{else: } K(w,j) = \max{ \{K(w,j-1), K(w-w_j, j-1)+v_j \}}$
$ \texttt{return }K(W,n)$
- 위 알고리즘은 $(W+1, n+1)$ 크기의 2차원 테이블에서 탐색
- 테이블 내 성분 하나는 constant time 내 연산 수행
$\therefore$ $O(nW)$ 시간만큼 걸림 (첫번째 케이스랑 동일)
Memoization (183p)
- 생략
6.5 Chain matrix multiplication
문제 상황
- 4개의 행렬 $A,B,C,D$에 대해서, $A\times B \times C \times D$ 행렬 곱을 하려고 한다.
- 행렬 곱은 $commutative$하지는 않지만, $associative$하다.
- 어떻게 묶느냐(parenthesize)에 따라서, 곱셈하는 방식이 다를 수 있다.

- 두 행렬($m \times n$, $n \times i$)을 곱할 때, 필요한 연산량은 $mni$
- 위 그림에서 볼 수 있듯이, greedy 접근은 실패할 수도 있음(매번 the cheapest matrix multiplication을 선택)
- $A_1 \times A_2 \times \cdots \times A_n$를 계산하고 싶을 때, optimal order을 어떻게 결정하는 것이 좋을까?
- 여기서 $A_i, i \in {1,…,n}$는 각각, $m_0 \times m_1, m_1 \times m_2, … , m_{n-1} \times m_n$의 차원을 가지는 행렬을 의미함.
- 먼저, parenthesization은 자연스럽게 binary tree로 표현할 수 있다는 것을 이해해야 함
- leaves가 개별 행렬로 표시되고, root가 최종 행렬곱을 의미한다.
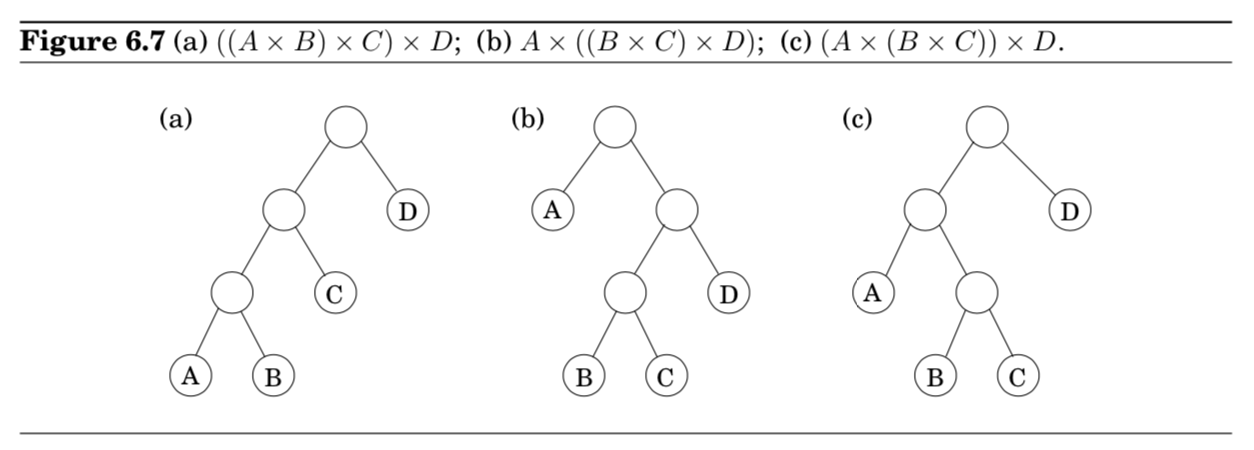
- 각각의 트리에 대해 해보는 방법말고, DP로 눈을 돌려보자.
The view of Dynammic Programming
- Figure 6.7에서 볼 수 있듯이, 어떤 트리가 OPT면, 그 트리의 서브트리도 OPT일 수 밖에 없다.
- 서브트리에 해당하는 subproblems를 어떻게 나타낼 수 있을까?
- 바로 $A_i \times A_{i+1} \times \cdots \times A_j$에 해당함
- 더 구체적으로 표현해보면, subproblem을 다음과 같이 정의할 수 있음 $\text{for } 1 \leq i \leq j \leq n, \; C(i,j) = \text{minimum cost of multiplying } A_i \times A_{i+1} \times \cdots \times A_j.$
- subproblem의 크기는 행렬곱의 횟수인 $|j-i|$
- 가장 작은 subproblem은 $i=j \Rightarrow C(i,i)=0$
- $j>i$에 대해, $C(i,j)$의 OPT 서브트리에 생각해보자.
- 이 서브트리의 가장 윗 지점인 첫 분기점은, 두 가지로 곱을 나눌 것임
- $A_i \times \cdots \times A_k$와 $A_{k+1} \times \cdots \times A_j, i \leq k < j$
- 즉, $C(i,j)$는 $C(i,k) + C(k+1, j) + m_{i-1} \cdot m_k \cdot m_j$ (마지막 항 = 두 행렬곱의 연산량)
- 이렇게 나누는 $k$값 중에서 가장 작은 값을 찾아야 하므로, 다음과 같은 최종 식을 만들 수 있음
- $C(i,j) = \min_{i \leq k < j} \{C(i,k)+C(k+1,j)+m_{i-1} \cdot m_k \cdot m_j\} $
Algorithm
$\texttt{for }i=1\texttt{ to } n: \;\;\;\; C(i,i)=0$
$\texttt{for }s=1\texttt{ to } n-1:$ s = #(matmul)
$\;\;\;\; \texttt{for }i=1\texttt{ to }n-s:$
$\;\;\;\;\;\;\;\; j=i+s$
$\;\;\;\;\;\;\;\; C(i,j) = \min{\{ C(i,k)+C(k+1,j)+m_{i-1}\cdot m_k \cdot m_j : i \leq k < j \}}$
$ \texttt{return } C(1,n)$
- subproblems는 2차원 테이블로 구성되어 있는 형태
- 각 성분마다, 총 $O(n)$ 연산량 필요
$\therefore$ 총, $O(n^3)$의 연산량이 필요하게 됨
6.6 Shortest paths
- chapter 6을 시작할 때, dag에서 최단경로를 찾는 기본적인 DP 알고리즘에 대해 살펴봤다.
- 좀 더 정교한 SP문제들을 다루면서, 강력한 DP를 어떻게 녹여낼 수 있는지 살펴보자.
Shortest reliable paths
- 문제 소개

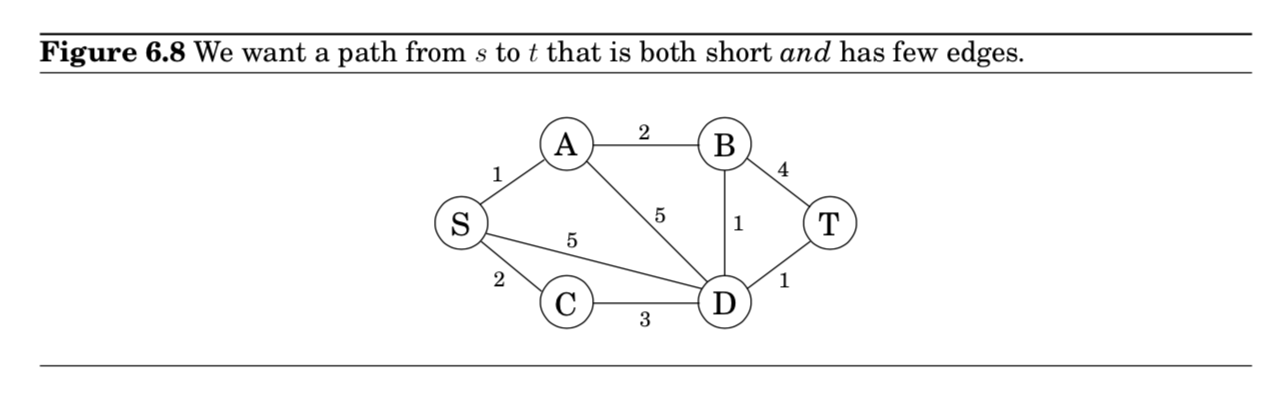
- 최단 경로에 가까우면서, 각 노드들을 최소한으로 거쳐가는 경로를 찾고 싶다.
- $S$에서 $T$로 가고 싶을 때, 최단 경로는 4개의 edges를 필요로 한다.
- 조금 더 길지만, 2개의 edges로만 가는 경로도 있다.
- 문제 정의
- edge에 길이가 존재하는 graph $G$가 주어졌다고 하자.
두 노드 $s$와 $t$와 정수 $k$에 대해, 최대 $k$개의 edges를 사용해서 $s$에서 $t$로 가는 최단 경로를 찾고 싶다!
- edge에 길이가 존재하는 graph $G$가 주어졌다고 하자.
- 알고리즘 전개
- Q) 이 새로운 문제에 다익스트라 알고리즘을 적용할 수 있을까?
- A) 힘들듯 싶다.
- 다익스트라 알고리즘은 경로 내에 몇 개의 노드를 지나쳤는지(the number of nodes)를 “기억하지 않고”,
최단 경로의 길이에 초점을 맞춘 알고리즘이기 때문이다.
- 다익스트라 알고리즘은 경로 내에 몇 개의 노드를 지나쳤는지(the number of nodes)를 “기억하지 않고”,
- DP에서는 subproblems를 선택하는 방식으로 필수 정보를 기억하고 전달하는 트릭을 사용 가능
- DP 알고리즘
- 각 노드 $v$와 정수 $i \leq k$에 대해,
$\texttt{dist}(v,i)$를 $\text{the length of the shortest path from }s\text{ to }v\text{ that uses }i\text{ edges}$ 로 정의하자!!! - $\texttt{dist}(v,0)$은 모두 $\infty$로 정의하고, 정점 $s$에 대해서만 0으로 초기화.
- $\text{update}$ 하는 식을 자연스럽게 아래와 같이 정의하면 끝
- \[\texttt{dist}(v,i) = \min_{(u,v)\in{E}}{\{\texttt{dist}(u,i-1)+l(u,v)\}}\]
- 각 노드 $v$와 정수 $i \leq k$에 대해,
All-pairs shortest paths
- 문제 소개
- 모든 쌍에 대해 최단경로를 알고 싶다!
- 문제 소개 2
- 한 정점으로부터 모든 노드에 대해 최단 경로를 찾는 알고리즘을 각 노드($|V|$)마다 돌려도 되지 않을까?
- 음수 길이를 고려해, 벨만-포드 알고리즘을 사용해보자.
- 이 경우, 복잡도는 $O(|V|^2 |E|)$가 된다.
- 복잡도가 $O(|V|^3)$로 좀 더 나은 알고리즘을 알아보자.
- DP를 기반으로 만들어진 알고리즘
- 플로이드 와샬($Floyd$-$Warshall$) 알고리즘이라고 부름
- 한 정점으로부터 모든 노드에 대해 최단 경로를 찾는 알고리즘을 각 노드($|V|$)마다 돌려도 되지 않을까?
- 알고리즘 전개
- $u$와 $v$ 사이 최단경로인 $u \rightarrow w_1 \rightarrow \cdots \rightarrow w_l \rightarrow v$는 몇 개의 중간 노드를 가질 수도 있고, 아예 없을 수도 있음
- $w_1,…, w_l$과 같은 중간 노드들을 허용하지 않는다고 가정하자.
- 그렇다면, all-pairs shortest paths는 한 번에 해결 가능함
- $u$에서 $v$로 가는 최단 경로는 단순히 그들 사이의 edge $(u,v)$라고 할 수 있음, 연결된 경우라면
- 만약 우리가 계속해서 set of permissible intermediate nodes를 늘려간다고 한다면?
- 각 단계에서 shortest path lengths를 updating함
- 결과적으로, 이 집합은 $V$의 모든 노드들을 포함하게 된다.
- 각 경로들은 모든 노드들을 포함하게 된다는 뜻이므로,
- 그래프의 노드들 간의 최단 경로들을 찾을 수 있을 것이다!
- 그렇다면, all-pairs shortest paths는 한 번에 해결 가능함
- 이 아이디어를 구체적으로 전개
- $V$에 있는 노드들을 ${1,2,..,n}$라 하자.
- $\texttt{dist}(i,j,k)$는 오직 ${1,2,…,k}$만을 중간 노드(intermediate)로 사용해 $i$에서 $j$로 가는 최단 경로의 길이를 말함
- 따라서, $\texttt{dist}(i,j,0)$은 $i$와 $j$의 direct edge의 길이가 된다. direct edge가 없는 경우, $\infty$로 설정
- 만약에 extra node $k$를 포함시켜 intermediate set을 확장시킬 때 어떤 일이 발생할까?
- 모든 $i,j$쌍에 대해서 다시 조사를 해야 한다.
- = $k$를 중간 노드로 사용함으로써 $i$에서 $j$로 가는 더 짧은 경로를 줄 수 있는지 여부를 체크해야 함
- $k$를 사용하면서 $i$에서 $j$로 가는 최단 경로는 $k$를 한 번밖에 안지남 (왜? negative cycles이 없기 때문에!)
- 이미, $k$보 낮은 노드들을 사용하면서 $i$에서 $k$로 가는 최단 경로 길이와, $k$에 $j$로 가는 최단 경로 길이는 계산했었음
- 각각 $\texttt{dist}(i,k,k-1)$, $\texttt{dist}(k,j,k-1)$을 의미함
- 따라서, $k$를 사용함으로써, $i$에서 $j$로 가는 최단 경로가 업데이트 되는 경우는 다음과 같다.
- $\texttt{dist}(i,k,k-1)$ + $\texttt{dist}(k,j,k-1)$ < $\texttt{dist}(i,j,k-1)$
- 알고리즘 $O(|V|^3)$
$\texttt{for }i=1\texttt{ to }n:$
$\;\;\;\; \texttt{for }j=1\texttt{ to }n:$
$\;\;\;\;\;\;\;\; \texttt{dist}(i,j,0)=\infty$
$\texttt{for all }(i,j)\in E:$
$\;\;\;\; \texttt{dist}(i,j,0)=l(i,j)$
$\texttt{for }k=1\texttt{ to }n:$
$\;\;\;\; \texttt{for }i=1\texttt{ to }n:$
$\;\;\;\;\;\;\;\; \texttt{for }j=1 \texttt{ to }n:$
$\;\;\;\;\;\;\;\;\;\;\;\; \texttt{dist}(i,j,k)=\min{\{\texttt{dist}(i,k,k-1)+\texttt{dist}(k,j,k-1), \texttt{dist}(i,j,k-1) \}}$
The traveling salesman problem(TSP)
- 문제 상황(구체화)
- 각 도시들을 $1,…,n$이라고 적고, salesman의 hometown을 1이라고 하자.
- $D=(d_{ij})$는 intercity distacnes matrix라고 하자.
- (목표) 1에서 출발해서 1로 끝나는데, 모든 도시를 정확히 한 번씩 포함시키면서 최단 이동경로로 움직여야 함

- 위 그림은 $n=5$인 경우인데, OPT tour를 찾아내려고 해도 쉽지 않다.
- TSP의 Complexity
- TSP 문제는 사실 notorious computational task임
- 가장 쉽게 brute-force로 접근하는 방식이 있음
- 모든 경우의 수를 측정해서 가장 좋은 경로를 뱉어내면 됨
- 도시가 $n$개 일 때, $(n-1)!$의 가능성이 있으므로, $O(n!)$의 시간 복잡도를 가지게 됨
- DP를 이용하면, 더 빠르게 솔루션을 찾을 수 있음. (but not polynomial)
- the view of Dynammic Programming
- TSP의 적절한 subproblem이 뭘까?
- 우리가 1번 도시에서 시작해서, 몇 개의 도시를 지나 $j$라는 도시에 현재 있다고 가정하자.
- 이 부분 경로를 확장하기 위해 어떤 정보가 우리에게 필요할까?
- 어떤 도시가 다음에 방문하기 가장 편한지 결정해야하기 때문에, $j$에 대해 확실히 알 필요는 있다.
- 그리고 우리는 방문했던 모든 도시들을 알아야 한다. (중복을 피하기 위해서)
- 1과 $j \in S$ 를 포함하는 도시들의 부분집합 $S \subseteq {1, 2, …, n}$에 대해서, $C(S,j)$를 다음과 같이 정의한다.
시작이 1이고, 종점이 $j$이면서 $S$ 안의 모든 노드들을 한번씩 방문한 최단 경로의 길이라고 하자. - $|S|>1$일 때, $C(S,1)=\infty$로 정의하자. ($C({1},1)=0$ 이 됨)
- 예시) 우리가 1에서 출발해서 $j$에서 끝냈다고 하자.
- $j$ 직전의 어떤 도시를 선택할 경우, $j$까 어떤 경로로 가야할지 결정하는 문제에 대해 생각해보자.
- 어떤 $i \in S$에 대해, 전체 경로 길이는 1에서 $i$까지가 될거기 때문에 $C(S-{j}, i)$가 되고, 마지막으로 $i$에서 $j$로 가는 edge length인 $d_{ij}$를 더하면 된다. 그리고 그 $i$는 best such $i$를 뽑아야 하므로 아래와 같은 식이 된다.
- $C(S,j) = \min_{i \in S, i \neq j}{C(S-\{j\},i) + d_{ij}}$
- The subproblems are ordered by $|S|$
- TSP의 적절한 subproblem이 뭘까?
- 알고리즘 $O(n^2 2^n)$

- 최대 $2^n \cdot n$ 개의 subproblem이 존재하고, 각 문제를 풀 때 linear time이 걸린다.
- 따라서 $O(n^2 2^n)$
On time and memory
- DP algorithm을 실행할 때 걸리는 시간은 subproblems의 dag로부터 알아내기 쉽다.
- 대부분의 경우, dag 안에 edges 총 개수다!
- linearized 순서로 정렬된 노드들을 방문하면서, 각 노드의 inedges를 조사하고, 각 edge마다 constant 작업을 하는 경우가 많다.
- 따라서 끝까지 갔을 때, DAG의 각 edge는 한 번씩 조사된다고 볼 수 있다.
- 시간복잡도가 아니라 공간복잡도에 대해 생각해보자.
- 컴퓨터 메모리가 얼마나 필요한가?
- 확실히, subproblems의 개수만큼 = 노드의 숫자에 비례한 만큼 메모리를 사용하면 가능함
- 하지만, 더 큰 subproblems를 풀 때까지만 기억하면 되기 때문에 더 작게 쓸 수 있음
- 예시)
- 플로이도 와샬 알고리즘에서 dist(i,j,k) 값은 dist(.,.,k+1)이 계산되고 나면 필요없는 값임
- 따라서, dist(i,j,k)를 계산할 때 dist(i,j,k-2)를 overwrite하는 구조로 사용하게 됨
따라서, 2개의 V * V 배열이 필요한다고 할 수 있다. - 하나는 짝수 번째 dist 값 저장
- 다른 하나는 홀수 번째 dist 값 저장
- 그렇다면, Figure 6.5에 있는 edit distance dag가 왜 더 짧은 문자열의 길이에 비례하는 메모리가 필요한지 설명해보세요!
6.7 Independent sets in trees
independent set이란?

- A subset of nodes $S \subset V$ is an independent set of graph $G=(V,E)$ if there are no edges between them.
- 즉, 서로 인접하지 않는 노드들의 집합을 뽑는 것
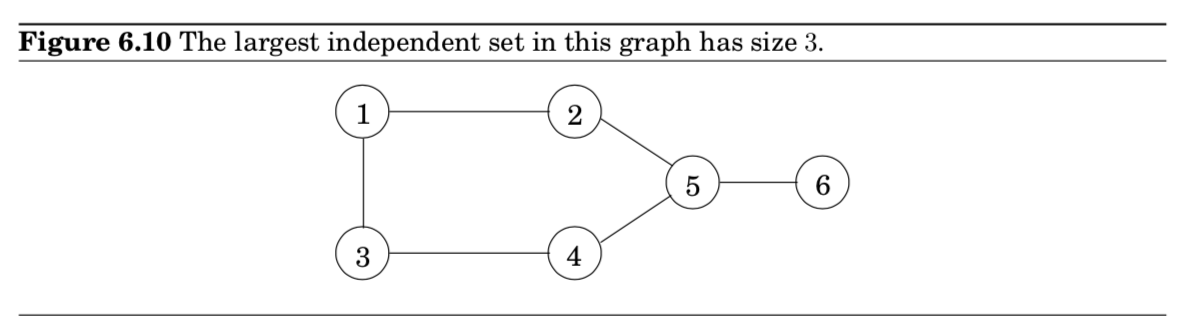
- 예시) {1,5}=가능, {1,4,5}=불가능, {2,3,6}=가능+가장 큰 indep. set임
문제 구체화
- 주어진 그래프에서 the largest independent set을 찾아라
- 근데, 그래프가 트리 구조라면, DP를 이용해서 linear time 안에 찾을 수 있다!
- (항상 그래왔듯이) subproblem을 어떻게 정의해야할까?
- chain matrix multiplication 문제를 떠올려 봅시다.
- 트리의 레이어 구조를 자연스럽게 subproblem의 정의로 가져올 수 있지 않을까? (자연스럽게…?)
- (트리의 어떤 노드를 루트 노드로 식별할 수만 있다면…)
알고리즘 전개
- 아무 노드 $r$을 root로 잡고, 트리를 전개한다.
- 이제 각 노드를 서브트리로 정의할 수 있게 된다.
- 그 노드 밑으로 걸려 있는 트리로 생각하면 된다.
- subproblem
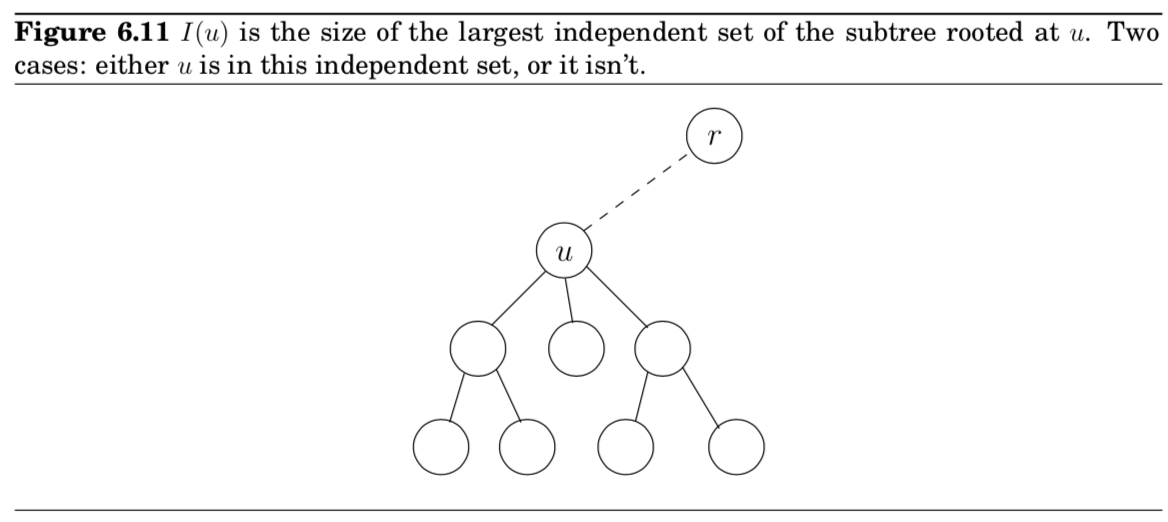
- $I(u) = \text{size of largest indep. set of subtree hanging from }u$
- Our final goal
- $I(r)$
- DP는 rooted tree에서 bottom-up 방식으로 접근
- 특정 노드 $u$ 밑에 모든 자식 노드들 $w$의 $I(w)$값을 안다고 하자.
- 그렇다면, 노드 $u$의 $I(u)$를 어떻게 계산할 수 있을까?
- 2가지 경우로 생각하면 끝
- 1) $u$가 포함되는 경우
- 2) $u$가 포함되지 않는 경우

- 1) 의 경우 = $u$의 자식 노드들은 포함되지 않았다는 뜻 = 자식의 자식 노드들의 $I(w)$ 합에 +1($u$가 추가될 것임)
- 2) 의 경우 = $u$의 자식 노드들의 $I(w)$ 합을 그대로 들고옴
- 2가지 경우로 생각하면 끝
- 따라서, \(I(u) = \max{ \{ 1 + \sum_{\text{grandchildren }w \text{ of } u}I(w), \sum_{\text{children }w \text{ of }u} I(w) \}}\)
알고리즘 분석
- subproblems의 개수는 vertices의 개수와 정확히 동일하다.
- 조금 더 신경쓰면, $O(|V|+|E|)$의 linear time으로 만들 수 있음
reference
Dynammic Programming
- http://web.mit.edu/broder/Public/6.006-exam.pdf
checkbox
- 6.1
- 6.2
- 6.3
- 6.4 Knapsack
- 6.5 Chain matrix multiplication
- parenthesization → DP (think about of subchain in matmuls)
- 6.6 Shortest paths
- 6.6.1 Shortest reliable paths
- 6.6.2 All pairs shortest paths
- 6.6.3 The traveling salesman problem
- 6.7 Independent set in trees
- rooted tree structure → DP (think about the diff. between child. and grandchild.)