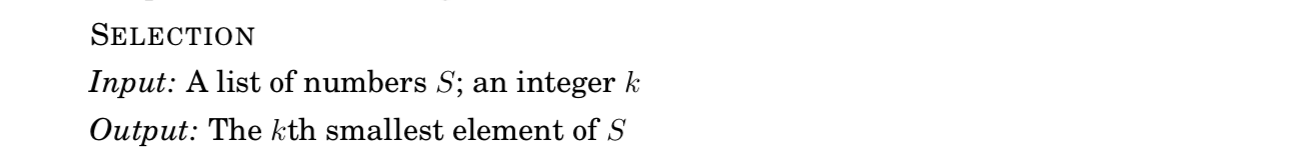해당 글은 Algorithms. by S. Dasgupta, C.H. Papadimitriou, and U.V. Vazirani 를 정리한 스터디 노트입니다.
Chapter 2 Divide-and-conquer algorithms
divide-and-conquer strategy
- 같은 유형의 더 작은 문제로 쪼개기
- 쪼갠 문제들을 재귀적으로 풀기
- 그 답들을 적절하게 합치기
2.1 Multiplication
두 복소수의 곱셈 CASE
\[(a+bi)(c+di) = ac - bd + (bc+ad)i\]- $ac, bd, bc, ad$ 라는 4번의 곱셈
→ $ac, bd, (a+b)(c+d)$ 라는 3번의 곱셈으로 줄임
( $\because bc + ad = (a+b)(c+d) - ac - bd$ ) - $\text{big-}O$ 방식의 thinking - 불필요한 곱셈 수를 줄이기
- 굉장히 낭비되는 ingenuity인 것처럼 보이지만, 재귀적으로 적용할 때 중요함
두 정수의 곱셈 CASE
\[x \times y\]- $x, y$ : $n$비트 정수
- 편의를 위해, $n$을 2의 지수로 생각
- 만약 $x = 10110110_2$ 라면 $x_L=1011_2, x_R=0110_2$
최종적으로 $x = 1011_2 \times 2^4 + 0110_2$ 로 표기
- $x$와 $y$의 곱을 계산하기 위해, 위와 같이 $n$비트에서 $n/2$비트로 split
- 덧셈은 linear time 이므로, 곱셈이 중요한 연산
- 4가지의 $n/2$비트 곱셈 : $x_{L}y_{L}, x_{L}y_{R}, x_{R}y_{L}, x_{R}y_{R}$ (=즉, four subproblems)
- 4가지 곱셈연산에 대해 다시 recursively 하게 split연산 적용 가능

- $T(n)$ : $n$비트 인풋 기준 총 연산 시간
- 최종적으로 계산해보면, $O(n^2)$임
- 전통적인 곱셈 테크닉도 $O(n^2)$임
- 새로운 split 알고리즘을 만들어냈지만, 진전이 없음
- 위에서 본 Gauss’s trick 적용
- $x_{L}y_{L}, x_{R}y_{R}, (x_L + x_R)(y_L + y_R)$ 3번의 곱셈으로 줄임
- 최종적으로 계산해보면, $O(n^{1,.59})$
- 사실은, $3T(n/2+1)$임
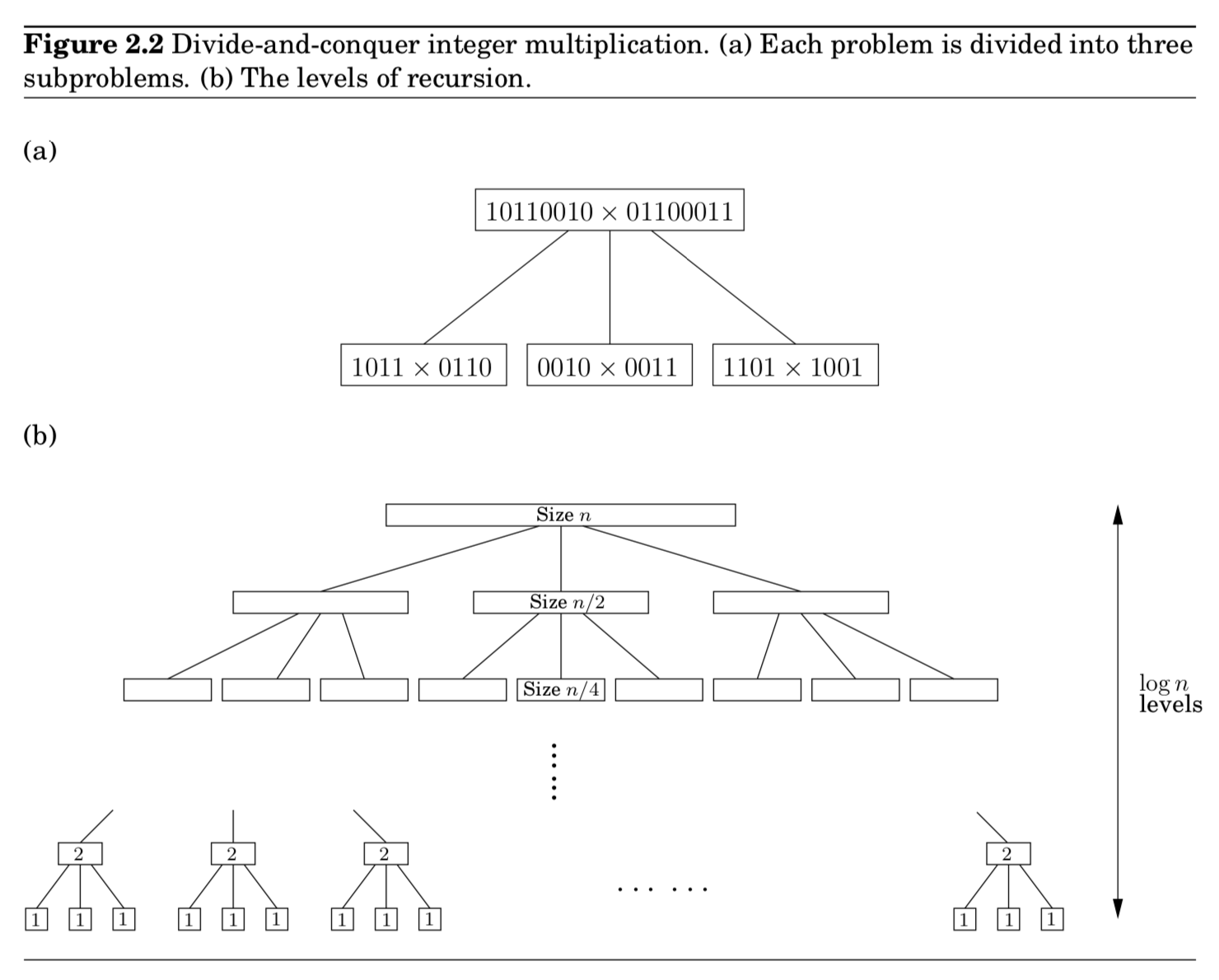
재귀적 호출의 알고리즘 패턴을 트리 구조로 해석 가능함
- 트리를 내려갈 때마다 사이즈는 반
- 트리를 내려갈 때마다 3개로 쪼개짐 (branching factor : 3)
- 트리의 높이 : $(log_2{n})$
- 트리가 $(log_2{n})^{th}$ 깊이로 갈 경우, 사이즈가 1이기 때문에 재귀 호출 종료
- $k$ 깊이에 잇는 총 연산 시간은 다음과 같음
→ $3^k \times O(\frac{n}{2^k}) = (\frac{3}{2})^k \times O(n)$ - 따라서 트리를 내려갈 때마다 geometrically $O(n)$부터 $O(n^{log_2{3}})$ 까지 연산량 증가
- 즉, 가장 많은 연산이 걸리는 곳이 트리의 마지막 깊이인 $log_2{n}$ 이므로 $O(n^{1.59})$ 가 되는 것
만약 4번의 곱셈처럼 기존의 하던대로 연산했다면?
- branching factor : 4
- 트리의 마지막 깊이 연산량 : $O(n^{log_2{4}})=O(n^2)$
A practical note
- 실제로, 1비트가 될 때까지 반복하지는 않는다.
- 대부분의 프로세서들은 16비트 혹은 32비트이므가 단일 연산 크기이므로, 그 때까지만 해당 알고리즘 적용됨
2.2 Recurrence relations
Divide-and-conquer 알고리즘의 패턴화
- $n$ 크기의 문제 하나를 만날 경우,
→ $a$ 개 서브문제들로 해석 (크기는 $n/b$ )
→ 이들을 결합하는 시간은 $O(n^d)$ 만큼의 시간- 실제로 우리가 했던 예제는 $a=3, b=2, d=1$ 이었음
- Running Time을 수식으로 나타내면,
$T(n) = aT([n/b]) + O(n^d) $
Master theorem : 패턴화를 바탕으로 closed-form solution을 도출
- $T(n) = aT([n/b]) + O(n^d) \text{ for some } contants \; a>0, b>1, \text{ and } d \geq 0, then \ $
\begin{cases} O(n^d) & if \; d > \text{log}_b{a} \
O(n^d{\text{log}n}) & if \; d = \text{log}_b{a} \
O(n^{\text{log}_b{a}}) & if \; d < \text{log}_b{a} \
\end{cases}
pf)
먼저, 편의상 $n$을 $b$ 제곱 형태로 가정
(걸쳐있는 경우에도 final bound에 중요하게 작용하지 않기 때문)- $k$ 단계 깊이일 때마다, 총 작업량은 다음과 같음
$a^k \times O(\frac{n}{b^k})^d = O(n^d) \times (\frac{a}{b^d})^k$- 재귀트리에서 각 레벨마다 factor $b$에 의해 subproblem으로 쪼개지므로 최종 $\text{log}_b{n}$ 깊이(단계)에서 base case에 도달한다는 것을 알 수 있음
- branching factor $a$에 의해 각 $k$ 단계일 때, 크기가 각각 $n/b^k$인 $a^k$개의 subproblems를 가짐을 알 수 있음
$k$가 0에서 $log_b{n}$까지 내려감에 따라, $a/b^d$ 비율의 geometric series를 생각할 수 있고, 이 series sum을 big-$O$ 노테이션에 의해 정리할 수 있음
- $a/b^d \leq 1$
- $a/b^d \geq 1$
- $a/b^d = 1$
Binary Search
- divide-and-conquer alogrithm을 결국 binary search라고 할 수 있음
- 예시) 정렬된 순서를 가진 $z[0, 1, …, n-1]$라는 하나의 큰 파일 속에서 $k$라는 키값을 찾고 싶음
1) 먼저 $k$를 $z[n/2]$와 비교함
2) 결과에 따라, 파일의 앞($z[0,…,n/2-1]$)을 볼지, 뒤($z[n/2,…,n-1]$)를 볼지 재귀적으로 체크 - 예시의 경우에는 $T(n) = T(\lceil{n/2}\rceil) + O(1)$
즉, $a=1, b=2, d=0$ case. - 실행시간은 $O(\text{log}{n})$을 가짐
2.3 Mergesort

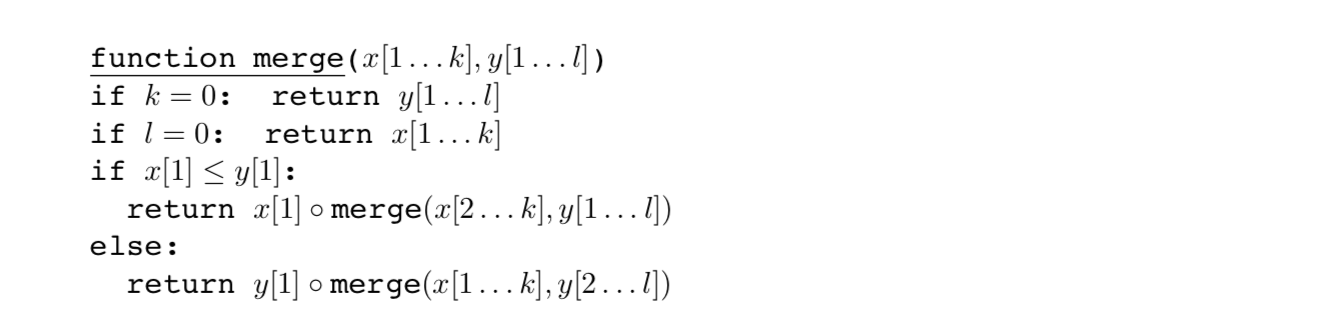
- mergesort를 호출할 때마다, 크기가 반씩 개수가 2개씩 늘어남 $T(n) \rightarrow 2T(n/2)$
- merge로 합칠 때마다, $O(k+l)$ 의 total running time이 필요함 → 즉, linear time $O(n)$
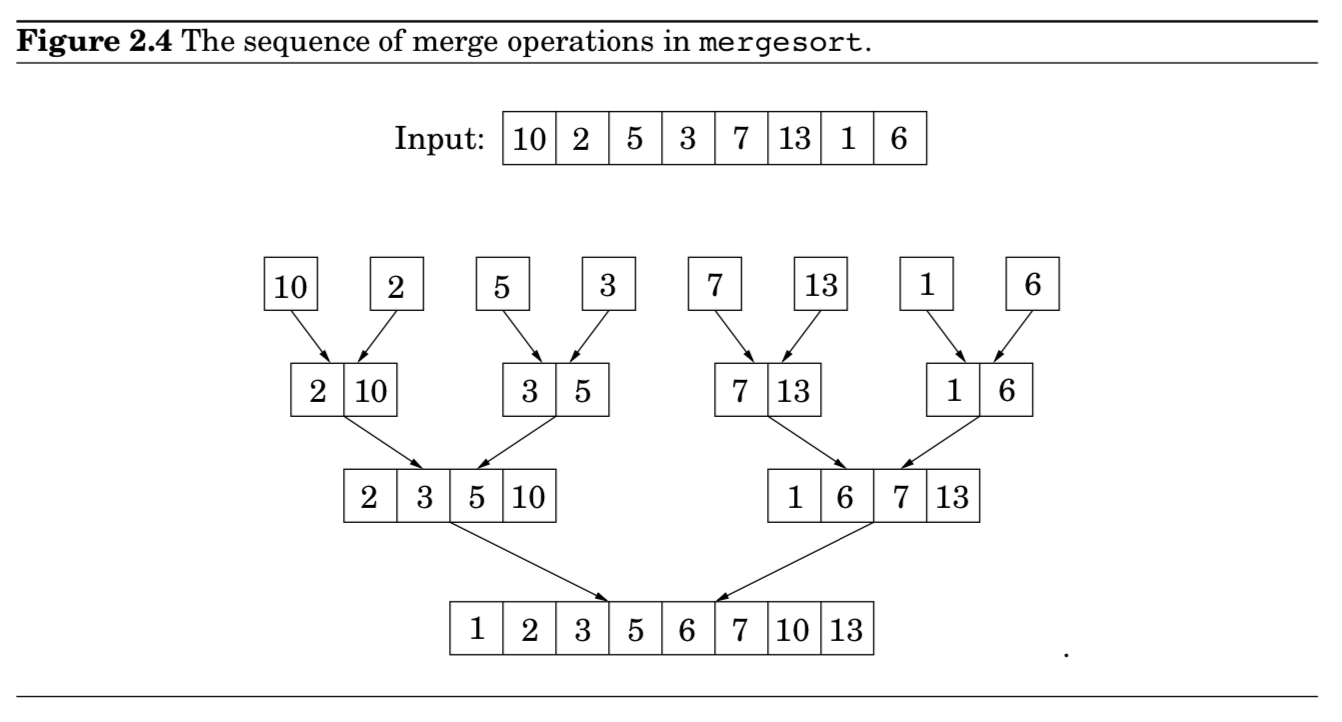
- 실제로 합쳐지는 과정은, singleton arrays로 떨어질 때까지 일어나지 않음
- singleton arrays = “active” arrays
- mergesort하는 과정을 queue구조를 사용해 iterative하게 만들 수도 있음 (recursively말고) 아래 참조

- inject : 큐의 마지막에 새로운 원소 추가(put)
- eject : 큐의 시작 원소를 제거하고 반환(get)
- 큐 구조 : FIFO (사람들이 줄 서있는 것을 생각)
An $n\text{log}n$ lower bound for sorting
정렬 알고리즘을 트리로 묘사 가능
- 이 때, 트리의 깊이는 the worst-case time complexity of the algorithm을 말함
- mergesort가 최적화되어 있다는 사실을 보여줄 때 유용함
- $n$개의 원소 정렬 시, $\Omega(n\text{log}n)$ 비교가 필수적인데, mergesort 충족
n-elements sorting algorithms
모든 permutation 형태가 leaves에 배치되어야 함
- binary tree이기 때문에 detph d는 최대 $2^d$개의 leaves를 가질 수 있음
- 즉, 트리 구조의 깊이(=알고리즘의 복잡도)는 최소 $\log(n!)$의 깊이를 가짐
- $\log{n!} \geq c \cdot n\log{n}$ for some $c>0$
- pf1. $n! \geq (n/2)^{(n/2)}$ ($\because n!$ 안에는 $n/2$보다 큰 숫자들이 $n/2$개 있으므로)
- pf2. Stirling’s formula
$n! \approx \sqrt{\pi(2n+\frac{1}{3})} \cdot n^n \cdot e^{-n}$
- 결론적으로, $n$ 개의 원소들을 정렬하는 어떤 comparison tree는 worst case가 $\Omega(n\text{log}n)$ 비교가 되어야 함.
- 따라서, mergesort는 이런 점에서 최적화!
2.4 Medians
중앙값을 찾기 위해 할 수 있는 제일 쉬운 방법은? Just Sorting
- 하지만…
- $O(n \text{log}n$) 이라는 시간이 걸림
- 중앙값을 제외한 나머지가 정렬되는데 초점을 맞추는 작업이 아님
Selection을 통해 해결

- 중앙값인 경우, $k = \lfloor |S| / 2 \rfloor$
A randomized divide-and-conquer algorithm for selection
리스트 $S$를 $v$ 라는 숫자에 의해 3가지 카테고리로 쪼갤 수 있음
- $S_L$ : $v$보다 작은 숫자들의 집합
- $S_v$ : $v$랑 같은 숫자들의 집합 (duplicates)
- $S_R$ : $v$보다 큰 숫자들의 집합
8번쨰로 작은 숫자를 찾고 싶은 경우?
- $|S_L| + |S_v| = 5$ 임을 통해 아래의 사실을 알 수 있음
- $\text{selection}(S,8) = \text{selection}(S_R,3)$
이를 일반화한다면, 다음과 같습니다.
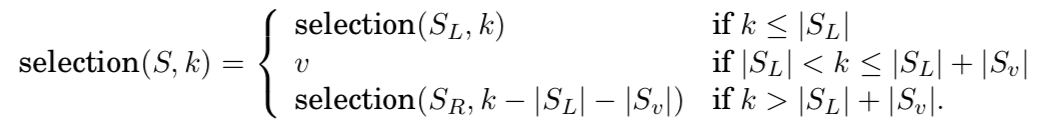
- $S$로부터 3가지 sublists들을 계산하는 것은 linear time
- $in \; place$ & without allocating (Exercise 2.15)
- 적절한 sublist를 찾을 때까지 반복함
- 쪼갬으로써 얻을 수 있는 효과는 기존 $|S|$를 $max{|S_L|, |S_R|}$까지 줄일 수 있다는 것
그렇다면, $v$는 어떻게 선택하는 것이 좋을까?
- 이상적인 케이스는 $|S_L|, |S_R| \approx \frac{1}{2}|S| $
- 즉, 반으로 잘 나눌 수 있는 $v$를 뽑았다면, 최종적으로 running time은 $T(n) = T(n/2) + O(n)$이 된다.
- 이 경우는, $v$를 중앙값으로 잘 뽑아야한다는 조건이 필요하지만, 더 간단한 대안으로 randomly하게 뽑을 것!
Efficiency analysis
이 알고리즘의 복잡도는 $v$를 어떻게 선택하는가에 달려있음
- Worst-case (매번 제일 큰 숫자나 작은 숫자 택하는 경우)
- 매 시간마다, 하나씩 줄일 수 있음
- $n + (n-1) + (n-2) + … + \frac{n}{2} = \Theta(n^2)$ , median을 계산하고 싶은 경우
- Best-case (한번에 반으로 나누는 경우)
- $O(n)$의 복잡도를 가짐 (모든 $n$에 대해 split하는 연산이 끝)
- 그렇다면, 평균적으로 어떤 복잡도를 가질까? 다행히, best-case에 가까움
50% 확률로 good으로 뽑을 수 있다고 한다면, good을 뽑기 위해 얼마나 많은 $v$를 시도해봐야할까?
- $v$가 25th-75th percentile에 들어오는 경우, $good$ 이라고 하자.
이러한 $v$를 선택할 경우, $S_L$과 $S_R$은 $S$의 최대 3/4 크기를 가짐 - Lemma에 의해, 평균적으로 2번 split operation을 한다면, 전체 리스트는 최대 3/4 크기로 줄어들음
- Lemma. On average a fair coin nedd to be tossed two times before a “heads” is seen.
- $T(n) \leq T(3n/4) + O(2n)$
- 즉, $T(n) = O(n)$
The Unix sort command
median-finding vs. mergesort
- mergesort는 생각없이 쪼개고 나서, 정렬하면서 합치는 구조
- Median-algorithm은 쪼갤 때 신중하게 쪼개는 구조
Quicksort $\approx$ median algorithm
- median algorithm이 동작하는 방식과 똑같음
- 배열의 pivot을 기준으로 배열을 나누고, 부분적으로 sorted하는 과정을 계속해서 반복하는 구조
- worst-case : $\Theta(n^2)$ (median-finding과 동일)
- 하지만, 평균적으로는 $O(n\log{n})$임 (Exercise 2.24)
- 다른 sorting algorithms보다 제일 빠름
2.5 Matrix multiplication
\[Z_{ij} = \sum_{k=1}^{n} X_{ik}Y_{kj}\]- 행렬곱에 있어서 $O(n^3)$ 복잡도를 가짐
- $n^2$개의 원소에 대해, 각 연산 $O(n)$을 실행해야하기 때문
- 이를 divide-and-conquer로 해결할 수 있음
- $n \times n$ 행렬을 $n/2 \times n/2$ 행렬로 쪼개어 생각함
- 따라서, $T(n) = 8T(n/2) + O(n^2)$
- 8번의 submatrix 곱과 $O(n^2)$ 복잡도의 덧셈 연산
- 기존 행렬 곱과 큰 차이가 없음
- 이를 7개의 subproblems로 쪼갤 수 있음 (by Volker Strassen)
- 자세한 implementation 생략
- 따라서, $T(n) = 7T(n/2) + O(n^2)$
- 최종적으로, 이는 $O(n^{\text{log}_2{7}}) \approx O(n^{2.81})$ by master theorem
2.6 The fast Fourier transform
(생략)
Exercises
2.3
2.13 Binary tree $full$
- $\text{Let }B_n \text{ denote the number of full binary trees with }n \text{ vertices.}$
- https://www.geeksforgeeks.org/enumeration-of-binary-trees/
- http://www.cs.rpi.edu/~moorthy/Courses/CSCI2300/csci2300-fall2014-test1-sol.pdf
2.24 Quicksort
2.28 The Hadamard matrices
2.29 Horner’s rule
2.32 CLOSEST PAIR
reference
Master Theorem
- https://www.youtube.com/watch?v=I7JCtSwVeXs
Median
- https://brilliant.org/wiki/median-finding-algorithm/
Merge / Quick sort
- https://gmlwjd9405.github.io/2018/05/08/algorithm-merge-sort.html
- https://gmlwjd9405.github.io/2018/05/10/algorithm-quick-sort.html
BST(binary search tree)
- https://ratsgo.github.io/data%20structure&algorithm/2017/10/22/bst/